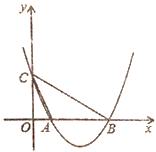
题目内容
【题目】本题共3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知数列![]() 满足
满足![]() .
.
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 是公比为
是公比为![]() 等比数列,
等比数列,![]() ,
,![]() 求
求![]() 的取值范围;
的取值范围;
(3)若![]() 成等差数列,且
成等差数列,且![]() ,求正整数
,求正整数![]() 的最大值,以及
的最大值,以及![]() 取最大值时相应数列
取最大值时相应数列![]() 的公差.
的公差.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的最大值为1999,此时公差为
的最大值为1999,此时公差为![]() .
.
【解析】
(1)依题意:![]() ,又
,又![]() 将已知代入求出x的范围;
将已知代入求出x的范围;
(2)先求出通项:![]() ,由
,由![]() 求出
求出![]() ,对q分类讨论求出Sn分别代入不等式
,对q分类讨论求出Sn分别代入不等式![]() Sn≤Sn+1≤3Sn,得到关于q的不等式组,解不等式组求出q的范围.
Sn≤Sn+1≤3Sn,得到关于q的不等式组,解不等式组求出q的范围.
(3)依题意得到关于k的不等式,得出k的最大值,并得出k取最大值时a1,a2,…ak的公差.
(1)依题意:![]() ,
,
∴![]() ;又
;又![]()
∴3≤x≤27,
综上可得:3≤x≤6
(2)由已知得,![]() ,
,![]() ,
,
∴![]() ,
,
当q=1时,Sn=n,![]() Sn≤Sn+1≤3Sn,即
Sn≤Sn+1≤3Sn,即![]() ,成立.
,成立.
当1<q≤3时,![]() ,
,![]() Sn≤Sn+1≤3Sn,即
Sn≤Sn+1≤3Sn,即![]() ,
,
∴![]()
不等式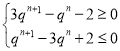
∵q>1,故3qn+1﹣qn﹣2=qn(3q﹣1)﹣2>2qn﹣2>0恒成立,
而对于不等式qn+1﹣3qn+2≤0,令n=1,
得q2﹣3q+2≤0,
解得1≤q≤2,又当1≤q≤2,q﹣3<0,
∴qn+1﹣3qn+2=qn(q﹣3)+2≤q(q﹣3)+2=(q﹣1)(q﹣2)≤0成立,
∴1<q≤2,
当![]() 时,
时,
![]() ,
,![]() Sn≤Sn+1≤3Sn,即
Sn≤Sn+1≤3Sn,即![]() ,
,
∴此不等式即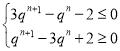 ,
,
3q﹣1>0,q﹣3<0,
3qn+1﹣qn﹣2=qn(3q﹣1)﹣2<2qn﹣2<0,
qn+1﹣3qn+2=qn(q﹣3)+2≥q(q﹣3)+2=(q﹣1)(q﹣2)>0
∴![]() 时,不等式恒成立,
时,不等式恒成立,
∴q的取值范围为:![]() .
.
(3)设a1,a2,…ak的公差为d.由![]() ,且a1=1,
,且a1=1,
得![]()
即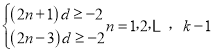
当n=1时,![]() d≤2;
d≤2;
当n=2,3,…,k﹣1时,由![]() ,得d
,得d![]() ,
,
所以d![]() ,
,
所以1000=k![]() ,即k2﹣2000k+1000≤0,
,即k2﹣2000k+1000≤0,
得k≤1999
所以k的最大值为1999,k=1999时,a1,a2,…ak的公差为![]() .
.

 阅读快车系列答案
阅读快车系列答案