题目内容

【题目】将正方形沿对角线折成直二面角，有如下四个结论：

①；

②是等边三角形；

③与平面所成的角为；

④与所成的角为.

其中错误的结论是____________.

【答案】③

【解析】

作出此直二面角的图象，由图形中所给的线面位置关系对四个命题逐一判断，即可得出正确结论．

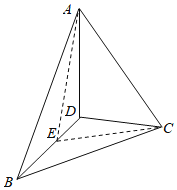
作出如图的图象，其中A﹣BD﹣C＝90°，E是BD的中点，可以证明出∠AED＝90°即为此直二面角的平面角

对于命题①，由于BD⊥面AEC，故AC⊥BD，此命题正确；

对于命题②，在等腰直角三角形AEC中可以解出AC等于正方形的边长，故△ACD是等边三角形，此命题正确；

对于命题③AB与平面BCD所成的线面角的平面角是∠ABE＝45°，故AB与平面BCD成60°的角不正确；

对于命题④可取AD中点F，AC的中点H，连接EF，EH，FH，由于EF，FH是中位线，可证得其长度为正方形边长的一半，而EH是直角三角形的中线，其长度是AC的一半即正方形边长的一半，故△EFH是等边三角形，由此即可证得AB与CD所成的角为60°；

综上知①②④是正确的

故答案为：③

练习册系列答案
相关题目

【题目】公元2222年，有一种高危传染病在全球范围内蔓延，被感染者的潜伏期可以长达10年，期间会有约0.05%的概率传染给他人，一旦发病三天内即死亡，某城市总人口约200万人，专家分析其中约有1000名传染者，为了防止疾病继续扩散，疾病预防控制中心现决定对全市人口进行血液检测以筛选出被感染者，由于检测试剂十分昂贵且数量有限，需要将血样混合后一起检测以节约试剂，已知感染者的检测结果为阳性，末被感染者为阴性，另外检测结果为阳性的血样与检测结果为阴性的血样混合后检测结果为阳性，同一检测结果的血样混合后结果不发生改变.

（1）若对全市人口进行平均分组，同一分组的血样将被混合到一起检测，若发现结果为阳性， 则再在该分组内逐个检测排査，设每个组个人，那么最坏情况下，需要进行多少次检测可以找到所有的被感染者？在当前方案下，若要使检测的次数尽可能少，每个分组的最优人数？

（2）在（1）的检测方案中，对于检测结果为阳性的组来取逐一检测排査的方法并不是很好， 或可将这些组的血样再进行一次分组混合血样检测，然后再进行逐一排査，仍然考虑最坏的情况，请问两次要如何分组，使检测总次数尽可能少？

（3）在（2）的检测方案中，进行了两次分组混合血样检测，仍然考虑最坏情况，若再进行若干次分组混合血样检测，是否会使检测次数更少？请给出最优的检测方案.

【题目】设函数，曲线在点处的切线方程为.

（1）求的解析式；

（2）证明：曲线上任一点处的切线与直线和直线所围成的三角形面积为定值，并求此定值.

【题目】如图，在四棱锥中，底面是边长为的正方形， 为等边三角形， ， 分别是， 的中点， .

（Ⅰ）求证：平面平面；

（Ⅱ）求点到平面的距离.

【题目】已知有限集合，定义如下操作过程：从中任取两个元素、，由中除了、以外的元素构成的集合记为；①若，则令；②若，则；这样得到新集合，例如集合经过一次操作后得到的集合可能是也可能得到等，可继续对取定的实施操作过程，得到的新集合记作，……，如此经过次操作后得到的新集合记作，设，对于，反复进行上述操作过程，当所得集合只有一个元素时，则所有可能的集合为______．

【题目】“石头、剪刀、布”，又称“猜丁壳”，是一种流行多年的猜拳游戏，起源于中国，然后传到日本、朝鲜等地，随着亚欧贸易的不断发展，它传到了欧洲，到了近代逐渐风靡世界．其游戏规则是：出拳之前双方齐喊口令，然后在语音刚落时同时出拳，握紧的拳头代表“石头”，食指和中指伸出代表“剪刀”，五指伸开代表“布”．“石头”胜“剪刀”、“剪刀”胜“布”、而“布”又胜过“石头”．若所出的拳相同，则为和局．小军和大明两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛，则小军和大明比赛至第四局小军胜出的概率是（ ）

A. B. C. D.

【题目】已知正三棱柱中， 分别为的中点，设.

（1）求证：平面平面；

（2）若二面角的平面角为，求实数的值，并判断此时二面角是否为直二面角，请说明理由.

【题目】本题共3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分.

已知数列满足.

（1）若，求的取值范围；

（2）若是公比为等比数列，，求的取值范围；

（3）若成等差数列，且，求正整数的最大值，以及取最大值时相应数列的公差.

【题目】已知函数，令.

（1）当时，求函数的单调递增区间；

（2）若关于的不等式恒成立，求整数的最小值；

（3）若，正实数满足，证明： .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网