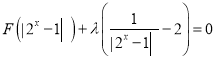题目内容
【题目】已知函数![]()
![]() ,且满足
,且满足![]() .
.
(1)判断函数![]() 在
在![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)设函数![]() ,求
,求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若存在实数m,使得关于x的方程![]() 恰有4个不同的正根,求实数m的取值范围.
恰有4个不同的正根,求实数m的取值范围.
【答案】(1)见解析(2) ![]() 时,
时, ![]() . (3)
. (3) ![]()
【解析】试题分析:(1)根据![]() 确定a.再任取两数,作差,通分并根据分子分母符号确定差的符号,最后根据定义确定函数单调性(2)先根据绝对值定义将函数化为分段函数,都可化为二次函数,再根据对称轴与定义区间位置关系确定最值,最后取两个最大值中较大值(3)先对方程变形得
确定a.再任取两数,作差,通分并根据分子分母符号确定差的符号,最后根据定义确定函数单调性(2)先根据绝对值定义将函数化为分段函数,都可化为二次函数,再根据对称轴与定义区间位置关系确定最值,最后取两个最大值中较大值(3)先对方程变形得![]() ,设
,设![]() ,转化为方程方程
,转化为方程方程![]() 在
在![]() 有两个不等的根
有两个不等的根![]() ,根据二次函数图像,得实根分布条件,解得实数m的取值范围.
,根据二次函数图像,得实根分布条件,解得实数m的取值范围.
试题解析:(1) 由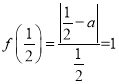 ,得
,得![]() 或0.
或0.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
当![]() 时,
时, ![]() ,任取
,任取![]() ,且
,且![]() ,
,
则![]()
![]()
![]() ,
,
因为![]() ,则
,则![]() ,
, ![]() ,
,
所以![]() 在
在![]() 上为增函数;
上为增函数;
(2)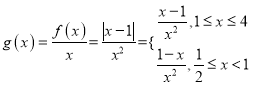 ,
,
当![]() 时,
时, ![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ,
,
因为![]() 时,所以
时,所以![]() ,所以当
,所以当![]() 时,
时, ![]() ;
;
综上,当![]() 即
即![]() 时,
时, ![]() .
.
(3)由(1)可知, ![]() 在
在![]() 上为增函数,当
上为增函数,当![]() 时,
时, ![]() .
.
同理可得![]() 在
在![]() 上为减函数,当
上为减函数,当![]() 时,
时, ![]() .
.
方程![]() 可化为
可化为![]() ,
,
即![]() .
.
设![]() ,方程可化为
,方程可化为![]() .
.
要使原方程有4个不同的正根,
则方程![]() 在
在![]() 有两个不等的根
有两个不等的根![]() ,
,
则有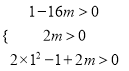 ,解得
,解得![]() ,
,
所以实数m的取值范围为![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目