题目内容
本小题满分12分)
已知抛物线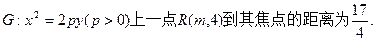
(I)求p与m的值;
(II)若斜率为—2的直线l与抛物线G交于P、Q两点,点M为抛物线G上一点,其横坐标为1,记直线PM的斜率为k1,直线QM的斜率为k2,试问: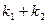 是否为定值?请证明你的结论。
是否为定值?请证明你的结论。
已知抛物线
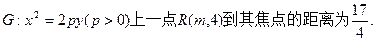
(I)求p与m的值;
(II)若斜率为—2的直线l与抛物线G交于P、Q两点,点M为抛物线G上一点,其横坐标为1,记直线PM的斜率为k1,直线QM的斜率为k2,试问:
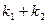 是否为定值?请证明你的结论。
是否为定值?请证明你的结论。解:(Ⅰ)根据抛物线定义,点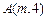 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即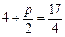 ,
,
解得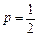 , ………………3分
, ………………3分
∴抛物线方程为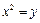 ,
,
点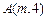 在抛物线上,得
在抛物线上,得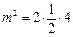 ,∴
,∴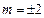 。………………5分
。………………5分
(Ⅱ)设直线 的方程为
的方程为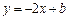 ,设
,设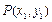 ,
,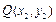 ,
,
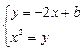 消元化简得
消元化简得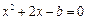 ,
,
当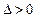 即
即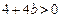 即
即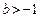 时,直线
时,直线 与抛物线有两交点,
与抛物线有两交点,
∴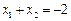 。 ………………7分
。 ………………7分
点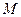 坐标为(1,1) ,
坐标为(1,1) , ,
,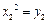 ,
,
∴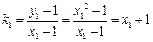 ,
, 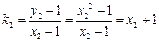 ,……………… 9分
,……………… 9分
∴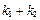
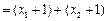
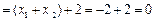 ,………………11分
,………………11分
所以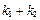 为定
为定 值。 ………………12分
值。 ………………12分
或: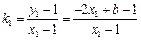 ,
,  ,
,
∴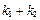
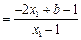
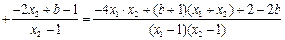
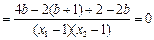 ,所以
,所以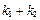 为定值。
为定值。
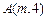 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即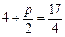 ,
,解得
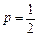 , ………………3分
, ………………3分∴抛物线方程为
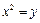 ,
,点
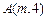 在抛物线上,得
在抛物线上,得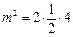 ,∴
,∴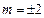 。………………5分
。………………5分(Ⅱ)设直线
 的方程为
的方程为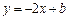 ,设
,设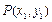 ,
,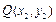 ,
,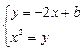 消元化简得
消元化简得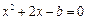 ,
,当
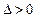 即
即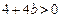 即
即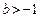 时,直线
时,直线 与抛物线有两交点,
与抛物线有两交点,∴
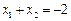 。 ………………7分
。 ………………7分点
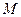 坐标为(1,1) ,
坐标为(1,1) , ,
,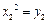 ,
,∴
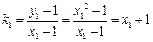 ,
, 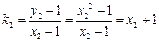 ,……………… 9分
,……………… 9分∴
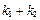
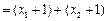
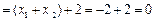 ,………………11分
,………………11分所以
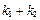 为定
为定 值。 ………………12分
值。 ………………12分或:
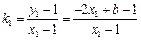 ,
,  ,
,∴
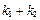
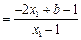
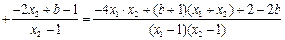
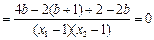 ,所以
,所以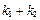 为定值。
为定值。略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
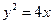 上一点P(
上一点P(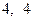 ),作两条直线分别交抛物线于A(
),作两条直线分别交抛物线于A(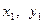 ),B(
),B(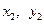 ).直线PA与PB的斜率存在且互为相反数,(1)求
).直线PA与PB的斜率存在且互为相反数,(1)求 的值,(2)证明直线AB的斜率是非零常数.
的值,(2)证明直线AB的斜率是非零常数.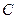 :
: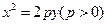 上一点
上一点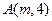 到其焦点的距离为
到其焦点的距离为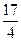 .
.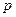 与
与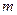 的值;
的值;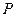 的横坐标为
的横坐标为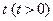 ,过
,过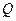 ,交
,交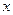 轴于点
轴于点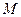 ,过点
,过点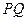 的垂线交
的垂线交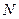 .若
.若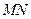 是
是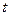 的最小值.
的最小值.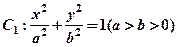 的左、右焦点分别为
的左、右焦点分别为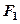 、
、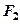 ,其中
,其中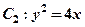 的焦点,M是
的焦点,M是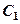 与
与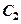 在第一象限的交点,且
在第一象限的交点,且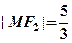 .
.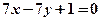 上,求直线AC的方程.
上,求直线AC的方程. 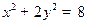 的一个焦点,则此抛物线的焦点到其准线的距离等于是 。
的一个焦点,则此抛物线的焦点到其准线的距离等于是 。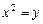 的焦点到准线的距离为______________.
的焦点到准线的距离为______________.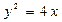 上一点P引抛物线准线的垂线,垂足为
上一点P引抛物线准线的垂线,垂足为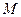 且
且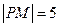 ,设抛物线的焦点为F,则
,设抛物线的焦点为F,则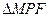 的面积为( )
的面积为( )
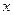 轴上的抛物线截直线
轴上的抛物线截直线 所得的弦长|AB|=
所得的弦长|AB|=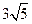 ,求此抛物线的方程。
,求此抛物线的方程。