题目内容
【题目】四棱柱![]() 的底面ABCD为矩形,AB=1,AD=2,
的底面ABCD为矩形,AB=1,AD=2,![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
【答案】C
【解析】分析:记A1在面ABCD内的射影为O,O在∠BAD的平分线上,说明∠BAD的平分线即菱形ABCD的对角线AC,求AC1的长.
解答:解:记A1在面ABCD内的射影为O,
∵∠A1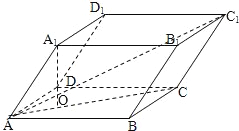 AB=∠A1AD,
AB=∠A1AD,
∴O在∠BAD的平分线上,
由O向AB,AD两边作垂线,垂足分别为E,F,连接A1E,A1F,A1E,A1F分别垂直AB,AD于E,F
∵AA1=3,∠A1AB=∠A1AD=60°,
∴AE=AF=![]()
又四棱柱ABCD-A1B1C1D1的底面ABCD为矩形
∴∠OAF=∠OAE=45°,且OE=OF=![]() ,可得OA=
,可得OA=![]()
在直角三角形A1OA中,由勾股定理得A1O=![]()
过C1作C1M垂直底面于M,则有△C1MC≌△A1OA,由此可得M到直线AD的距离是![]() ,M到直线AB的距离是
,M到直线AB的距离是![]() ,C1M=A1O=
,C1M=A1O=![]()
所以AC1 =![]() =
=![]()
故选C.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目