题目内容
6．已知F是抛物线y2=2px（p＞0）的焦点，G、H是抛物线上的两点，|GF|+|HF|=3，线段GF的中点到y轴的距离为$\frac{5}{4}$．（1）求抛物线的方程；
（2）如果过点P（m，0）可以作一条直线l，交抛物线于A、B两点，交圆（x-6）2+y2=4于C、D（自上而下依次为B、D、C、A），且$\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{PC}$+$\overrightarrow{PD}$，求实数m的取值范围．
分析 （1）由抛物线定义知：$\frac{5}{4}$+$\frac{p}{2}$=$\frac{3}{2}$，得p=$\frac{1}{2}$，即可求出抛物线的方程；
（2）由$\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{PC}$+$\overrightarrow{PD}$得$\overrightarrow{PA}$-$\overrightarrow{PC}$=$\overrightarrow{PD}$-$\overrightarrow{PB}$，即$\overrightarrow{CA}$=$\overrightarrow{BD}$，可得x1+x2=x4+x3，分类讨论，即可求实数m的取值范围．
解答 
解：（1）由抛物线定义知：$\frac{5}{4}$+$\frac{p}{2}$=$\frac{3}{2}$，得p=$\frac{1}{2}$…（2分）
故抛物线的方程为y2=x…（3分）
（2）由$\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{PC}$+$\overrightarrow{PD}$
得$\overrightarrow{PA}$-$\overrightarrow{PC}$=$\overrightarrow{PD}$-$\overrightarrow{PB}$，即$\overrightarrow{CA}$=$\overrightarrow{BD}$…（4分）
设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），
则$\overrightarrow{CA}$=（x1-x3，y1-y3），$\overrightarrow{BD}$=（x4-x2，y4-y2），
所以x1-x3=x4-x2，即x1+x2=x4+x3…（5分）
①当直线l的斜率不存在时，l的方程为x=m，此时只需点P（m，0）在圆内即可，
故（m-6）2＜4，解得4＜m＜8…（6分）
②当直线l的斜率存在时，设l的斜率为k，则l的方程为y=k（x-m）（且m≠0）
代入抛物线方程得：k2x2-（2mk2+1）x+m2k2=0…（7分）
因为直线l与抛物线于A、B两点，所以△1=4mk2+1＞0…①…（8分）
x1+x2=$\frac{2m{k}^{2}}{{k}^{2}}$
代入圆方程得：（1+k2）x2-2（mk2+6）x+m2k2+32=0
因为直线l与圆于C，D两点，所以△2＞0，即k2（m-6）2＜4（1+k2）…②…（9分）
x3+x4=$\frac{2m{k}^{2}+12}{1+{k}^{2}}$
因为x1+x2=x4+x3，所以$\frac{2m{k}^{2}}{{k}^{2}}$=$\frac{2m{k}^{2}+12}{1+{k}^{2}}$，化简得k2=$\frac{1}{11-2m}$…（10分）
代入①②得，解得-2＜m＜$\frac{11}{2}$…（11分）
综合得实数m取值范围为（-2，$\frac{11}{2}$）…（12分）
点评 本题考查抛物线的方程，考查直线与抛物线、圆的位置关系，考查韦达定理的运用，考查学生分析解决问题的能力，难度大．
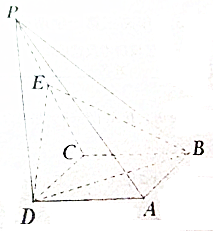如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠DBC=45°，$\frac{BD}{BC}$=$\sqrt{2}$，侧棱PD⊥底面ABCD，PD=CD，E是PC的中点．