题目内容
16.已知函数h(x)=lnx的反函数为φ(x),函数f(x)=φ(x)+ax2-x.(1)当a=0时,求函数f(x)的极值;
(2)设函数f(x)在点P(t,f(t))(0<t<1)处的切线为l,直线l与y轴相交于点Q,若点Q的纵坐标恒小于1,求实数a的取值范围.
分析 (1)当a=0时,f(x)=ex-x,f′(x)=ex-1,分别解出f′(x)>0,f′(x)<0,即可得出其单调区间和极值;
(2)利用导数的运算法则可得f′(x)=ex+2ax-1,利用导数的几何意义可得:函数f(x)在点P(t,f(t))(0<t<1)处的切线l的斜率,即可得到切线l的方程为y-(et+at2-t)=(et+2at-1)(x-t).令x=0,得y=(1-t)et-at2(0<t<1).当0<t<1时,要使得点Q的纵坐标恒小于1,只需(1-t)et-at2<1,即(t-1)et+at2+1>0(0<t<1).令g(t)=(t-1)et+at2+1,利用导数通过分类讨论即可得到其单调性.
解答 解:(1)函数h(x)=lnx的反函数为φ(x)=ex,
当a=0时,f(x)=ex-x,
导数f′(x)=ex-1,
当x>0时,f′(x)>0,f(x)递增;
当x<0时,f′(x)<0,f(x)递减.
即有x=0处取得极小值0,无极大值;
(2)∵f′(x)=ex+2ax-1,
∴函数f(x)在点P(t,f(t))(0<t<1)处的切线l的斜率k=f′(t)=et+2at-1,
∴切线l的方程为y-(et+at2-t)=(et+2at-1)(x-t),
令x=0,得y=(1-t)et-at2(0<t<1).
当0<t<1时,要使得点Q的纵坐标恒小于1,
只需(1-t)et-at2<1,即(t-1)et+at2+1>0(0<t<1).
令g(t)=(t-1)et+at2+1,
则g′(t)=t(et+2a),
∵0<t<1,∴1<et<e,
①若2a≥-1即a≥-$\frac{1}{2}$时,et+2a>0,
∴当t∈(0,1)时,g′(t)>0,即g(t)在(0,1)上单调递增,
∴g(t)>g(0)=0恒成立,∴a≥-$\frac{1}{2}$满足题意.
②若2a≤-e,即a≤-$\frac{e}{2}$时,et+2a<0.
∴当t∈(0,1)时,g′(t)<0,即g(t)在(0,1)上单调递减.
∴g(t)<g(0),∴a≤-$\frac{e}{2}$时不满足条件.
③若-e<2a<-1,即-$\frac{e}{2}$<a<-$\frac{1}{2}$时,0<ln(-2a)<1.列表如下:
| t | (0,ln(-2a)) | ln(-2a) | (ln(-2a),1) |
| g′(t) | - | 0 | + |
| g(t) | 单调递减 | 极小值 | 单调递增 |
综上①②③可得:当a≥-$\frac{1}{2}$时,g(t)>0,0<t<1.此时点Q的纵坐标恒小于1.
点评 本题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查分类与整合思想、数形结合思想、化归与转化思想.

| A. | a与β相交 | B. | a∥β | C. | a?β | D. | a∥β或a?β |
| A. | [-1,-$\frac{3}{4}$) | B. | (-∞,-1] | C. | (-$\frac{3}{4}$,0] | D. | [-1,0] |
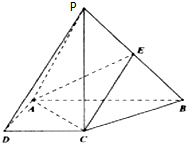 如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.