题目内容

1．在（1+2x）6（1+y）4展开式中，xy2项的系数为72．

分析 把题目中的式子利用二项式定理展开，即可得出xy2项的系数．

解答 解：∵（1+2x）6（1+y）4=（1+12x+60x2+160x3+…+64x6）（1+4y+6y2+4y3+y4），
∴xy2项的系数为12×6=72．
故答案为：72．

点评 本题考查了二项式定理的应用问题，也考查了二项式展开式通项公式的应用问题，是基础题目．

练习册系列答案
相关题目
11．若直线a⊥平面α，平面β⊥平面α，则a与β的位置关系为（　　）
A．a与β相交B．a∥βC．a?βD．a∥β或a?β
12．阅读如图的程序框图，运行相应的程序，若输入x的值为2，则输出y的值为（　　）
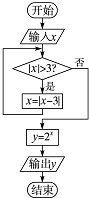
A．0.5B．1C．2D．4
9．已知向量$\overrightarrow{OA}$=（2，3），$\overrightarrow{OB}$=（-3，2）（O为坐标原点），若$\overrightarrow{AC}$=$\overrightarrow{BO}$，则向量$\overrightarrow{OC}$与$\overrightarrow{OB}$的夹角为135°．
16．设复数z1=1-2i（i为虚数单位），复数z2的实部为2，且z1•z2是实数，则z2•$\overline{{z}_{2}}$=（　　）
A．$\sqrt{5}$B．2$\sqrt{5}$C．20D．5
6．已知F是抛物线y2=2px（p＞0）的焦点，G、H是抛物线上的两点，|GF|+|HF|=3，线段GF的中点到y轴的距离为$\frac{5}{4}$．
（1）求抛物线的方程；
（2）如果过点P（m，0）可以作一条直线l，交抛物线于A、B两点，交圆（x-6）2+y2=4于C、D（自上而下依次为B、D、C、A），且$\overrightarrow{PA}$+$\overrightarrow{PB}$=$\overrightarrow{PC}$+$\overrightarrow{PD}$，求实数m的取值范围．
13．若函数f（x）=3|x-2|-m-2有唯一的零点，则直线mx+ky+3k-2=0恒过定点为（　　）
A．（$\frac{2}{7}，-3$）B．（-2，-3）C．（0，$\frac{2}{7}$）D．（-2，0）
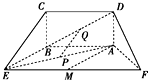10．对于函数y=f（x），x∈D，若对任意的x1∈D，存在唯一的x2∈D，使得$\sqrt{f（{x}_{1}）f（{x}_{2}）}$=M，则称函数f（x）在D上的几何平均数为M，已知f（x）=x3-x2+1，x∈[1，2]，则函数f（x）=x3-x2+1在[1，2]上的几何平均数M=$\sqrt{5}$．
11．如图所示的五面体中，四边形ABCD是矩形，AD⊥平面ABEF，AB∥EF，且AD=1，AB=$\frac{1}{2}$EF=2$\sqrt{2}$，AF=BE=2，点P、Q、M分别为AE、BD、EF的中点．
（1）求证：PQ∥平面BCE；
（2）求证：AM⊥平面ADF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网