题目内容
11.已知数列{an}满足anan+1=2n,a1=1,(1)求数列{an}的通项公式;
(2)Sn为数列{an}的前n项和,bn=$\frac{1}{3}$S2n,求所有的正整数m,使$\frac{{b}_{n+1}{b}_{n+1}}{{b}_{n}}$为整数.
分析 (1)通过anan+1=2n与an+1an+2=2n+1作商可知数列{an}的奇数项、偶数项分别构成以2为公比的等比数列,进而可得结论;
(2)通过(1)可知S2n=3(2n-1),进而可知$\frac{{b}_{n+1}{b}_{n+2}}{{b}_{n}}$=$\frac{({2}^{n+1}-1)({2}^{n+2}-1)}{{2}^{n}-1}$,利用换元法令2n-1=t可知$\frac{{b}_{m+1}{b}_{m+2}}{{b}_{m}}$=8•2m+2+$\frac{3}{{2}^{m}-1}$为整数,进而可得结论.
解答 解:(1)∵anan+1=2n,
∴an+1an+2=2n+1,
∴$\frac{{a}_{n+2}}{{a}_{n}}$=2,
∴数列{an}的奇数项、偶数项分别构成以2为公比的等比数列,
又∵a1=1,∴${a}_{2}=\frac{{2}^{1}}{{a}_{1}}$=2,
∴数列{an}的通项公式an=$\left\{\begin{array}{l}{{2}^{\frac{n-1}{2}},}&{n为奇数}\\{{2}^{\frac{n}{2}},}&{n为偶数}\end{array}\right.$;
(2)由(1)可知S2n=$\frac{1-{2}^{n}}{1-2}$+$\frac{2(1-{2}^{n})}{1-2}$=3(2n-1),
∴bn=$\frac{1}{3}$S2n=2n-1,
∴$\frac{{b}_{n+1}{b}_{n+2}}{{b}_{n}}$=$\frac{({2}^{n+1}-1)({2}^{n+2}-1)}{{2}^{n}-1}$,
记2n-1=t,则2n=t+1,
则$\frac{{b}_{m+1}{b}_{m+2}}{{b}_{m}}$=$\frac{(2t+1)(4t+3)}{t}$
=8t+10+$\frac{3}{t}$
=8•2m+2+$\frac{3}{{2}^{m}-1}$为整数,
故只有2m-1=1或3,即m=1或2.
点评 本题考查数列的通项及前n项和,注意解题方法的积累,属于中档题.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | f(x)的图象关于直线x=$\frac{5π}{12}$对称 | B. | f(x)的图象关于y轴对称 | ||
| C. | f(x)的最小正周期为2π | D. | f(x)在区间(0,$\frac{π}{3}$)单调递增 |
| A. | 6 | B. | -6 | C. | 7 | D. | -7 |
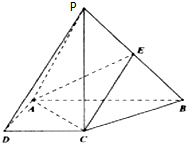 如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.
如图,在四棱锥P-ABCD.中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.