题目内容
15.已知函数f${\;}_{n}(x)={x}^{n}+(1-x)^{n},x∈(0,1),n∈{N}^{*}$.(Ⅰ)求证:21-n≤fn(x)≤1;
(Ⅱ)令b${\;}_{n}=\frac{3-2lo{g}_{3}{f}_{n}(x)}{1-lo{g}_{3}{f}_{n}(x)}$,求证:b1•b2…bn$>\sqrt{{2}^{2n}(n+1)}$.
分析 (Ⅰ)求出导数,求得单调区间,由单调性即可得证;
(Ⅱ)将bn化简,运用变量分离,再由(1)的结论,可得$\frac{1}{2}$bn≥$\frac{2n+1}{2n}$,由累乘法和$\frac{2n+1}{2n}$>$\frac{2n+2}{2n+1}$,运用放缩法,即可得证.
解答 证明:(Ⅰ)f′n(x)=nxn-1-n(1-x)n-1,当n≥2时,由f′n(x)>0可得$\frac{1}{2}$<x<1.
由f′n(x)<0可得0<x<$\frac{1}{2}$,即有fn(x)在区间(0,$\frac{1}{2}$]上单调递减,
在[$\frac{1}{2}$,1]上单调递增,则fn($\frac{1}{2}$)≤fn(x)≤max{fn(0),fn(1)}(n≥2),
即21-n≤fn(x)≤1;
(Ⅱ)bn=$\frac{3-2lo{g}_{2}{f}_{n}(x)}{1-lo{g}_{2}{f}_{n}(x)}$=3+$\frac{lo{g}_{2}{f}_{n}(x)}{1-lo{g}_{2}{f}_{n}(x)}$
=3+$\frac{1}{\frac{1}{lo{g}_{2}{f}_{n}(x)}-1}$,
由(Ⅰ)可得$\frac{1}{2}$bn≥$\frac{2n+1}{2n}$,
累乘,易得$\frac{1}{2}$b1•$\frac{1}{2}$b2•$\frac{1}{2}$b3…$\frac{1}{2}$bn≥$\frac{3}{2}$•$\frac{5}{4}$•$\frac{7}{6}$…$\frac{2n+1}{2n}$,
∵$\frac{2n+1}{2n}$>$\frac{2n+2}{2n+1}$,∴$\frac{3}{2}$>$\frac{4}{3}$,$\frac{5}{4}$>$\frac{6}{5}$,$\frac{7}{6}$>$\frac{8}{7}$,…,$\frac{2n+1}{2n}$>$\frac{2n+2}{2n+1}$,
∴$\frac{3}{2}$•$\frac{5}{4}$•$\frac{7}{6}$…$\frac{2n+1}{2n}$>$\frac{4}{3}$•$\frac{6}{5}$•$\frac{8}{7}$…$\frac{2n+2}{2n+1}$,
($\frac{3}{2}$•$\frac{5}{4}$•$\frac{7}{6}$…$\frac{2n+1}{2n}$)2>$\frac{3}{2}$•$\frac{4}{3}$•$\frac{5}{4}$…$\frac{2n+1}{2n}$•$\frac{2n+2}{2n+1}$=n+1,
即有$\frac{3}{2}$•$\frac{5}{4}$•$\frac{7}{6}$…$\frac{2n+1}{2n}$>$\sqrt{n+1}$,
则b1•b2…bn$>\sqrt{{2}^{2n}(n+1)}$成立.
点评 本题考查不等式的证明,注意运用导数判断单调性,由单调性证得,同时考查累乘法的运用,和放缩法证明不等式的方法,考查推理能力,具有一定的难度.

| A. | a?α,b⊥β,α∥β | B. | a⊥α,b⊥β,α∥β | C. | a∥α,b∥β,α⊥β | D. | a?α,b∥β,α⊥β |
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |

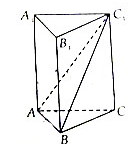 如图所示,在正三棱柱ABC-A1B1C1中,AB=1,CC1=$\sqrt{3}$.
如图所示,在正三棱柱ABC-A1B1C1中,AB=1,CC1=$\sqrt{3}$.