题目内容
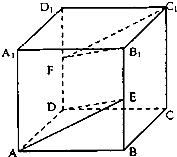
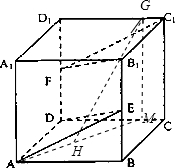
在正方体ABCD-A1B1C1D1中,棱长为1,E,F分别为棱BB1和DD1的中点.
(1)求证:平面B1FC1∥平面ADE;
(2)求四面体A1-FEA的体积.
(3)若G是C1D1上靠近C1的四等分点,动点H在底面ABCD内,且AH=
,请说明点H的轨迹,并探求GH长度的最小值.
(1)求证:平面B1FC1∥平面ADE;
(2)求四面体A1-FEA的体积.
(3)若G是C1D1上靠近C1的四等分点,动点H在底面ABCD内,且AH=
| 1 |
| 2 |

(1)∵E,F分别为棱BB1和DD1的中点,∴FD∥B1E,FD=B1E,
∴四边形FDEB1为平行四边形,∴DF∥FB1,DF?平面ADE,FB1?平面ADE,
∴FB1∥平面ADE,
又AD∥B1C1,AD?平面ADE,B1C1?平面ADE,∴B1C1∥平面ADE,
又FB1∩B1C1=B1,∴平面B1FC1∥平面ADE;
(2)连接EF、AF、A1F,A1E,
∴VA1-AEF=VE-A1AF=
×
×AA1×AD×AB=
×1×1×1=
;
(3)∵AH=
,动点H在底面ABCD内,∴点H的轨迹为
圆弧,
过G作GM⊥CD,垂足为M,∵MH≥MA-AH=
-
=
,
又GH=
≥
=
.
∴GH长度的最小值为
.
∴四边形FDEB1为平行四边形,∴DF∥FB1,DF?平面ADE,FB1?平面ADE,
∴FB1∥平面ADE,
又AD∥B1C1,AD?平面ADE,B1C1?平面ADE,∴B1C1∥平面ADE,
又FB1∩B1C1=B1,∴平面B1FC1∥平面ADE;
(2)连接EF、AF、A1F,A1E,
∴VA1-AEF=VE-A1AF=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
(3)∵AH=
| 1 |
| 2 |
| 1 |
| 4 |
过G作GM⊥CD,垂足为M,∵MH≥MA-AH=
(
|
| 1 |
| 2 |
| 3 |
| 4 |
又GH=
| GH2+MH2 |
12+(
|
| 5 |
| 4 |
∴GH长度的最小值为
| 5 |
| 4 |


练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
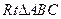 中,
中,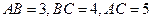 ,将三角形绕直角边
,将三角形绕直角边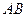 旋转一周所成
旋转一周所成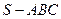 中,
中,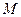 、
、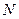 分别是棱
分别是棱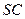 、
、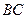 的中点,且
的中点,且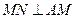 ,若侧棱
,若侧棱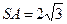 ,则正三棱锥
,则正三棱锥