题目内容
设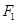
、
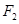是离心率为
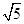的双曲线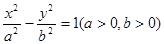
的左、右两个焦点，若双曲线右支上存在一点P，使
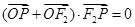（O为坐标原点）且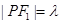
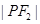则
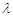的值为
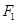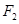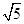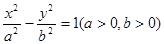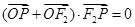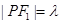
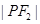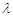、是离心率为的双曲线的左、右两个焦点，若双曲线右支上存在一点P，使（O为坐标原点）且则的值为| A．2 | B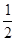． | C．3 | D． |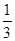
A
取PF2的中点A，推出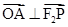
，由OA 是△PF1F2的中位线，得到PF1⊥PF2，由双曲线的定义求出|PF1|和|PF2|的值，进而在△PF1F2中，由勾股定理得及
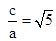，解得λ的值．
解：取PF2的中点A，则
∵(
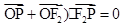∴2
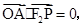
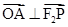，由 OA 是△PF1F2的中位线，
∴PF1⊥PF2，OA=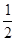PF1．
由双曲线的定义得|PF1|-|PF2|=2a，
∵|PF1|=λ|PF2|，∴|PF2|=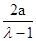
，|PF1|=λ?．
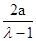△PF1F2中，由勾股定理得|PF1|2+|PF2|2=4C2，
∴(λ?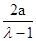)2+(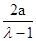)2=4c2，
又，∴(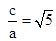
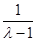) 2?(λ2+1) = 5，∴λ=2，
故选A．
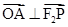，由OA 是△PF1F2的中位线，得到PF1⊥PF2，由双曲线的定义求出|PF1|和|PF2|的值，进而在△PF1F2中，由勾股定理得及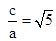，解得λ的值．解：取PF2的中点A，则
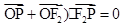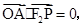
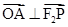∵(∴2，由 OA 是△PF1F2的中位线，∴PF1⊥PF2，OA=
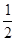PF1． 由双曲线的定义得|PF1|-|PF2|=2a，
∵|PF1|=λ|PF2|，∴|PF2|=
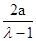，|PF1|=λ?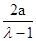．△PF1F2中，由勾股定理得|PF1|2+|PF2|2=4C2，
∴(λ?
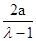)2+(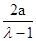)2=4c2，又
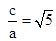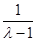，∴() 2?(λ2+1) = 5，∴λ=2，故选A．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
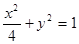共焦点且过点
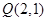的双曲线方程是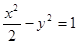
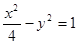
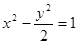
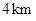的
，
两点，要围垦出以
为一条对角线的平行四边形区域建制造厂。按照规划，围墙总长为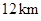
．在设计图纸上，建立平面直角坐标系如图（
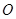为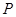
，
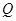的坐标满足的方程是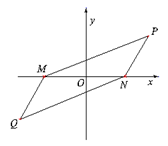
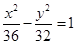
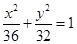
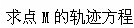
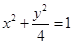，以椭圆的焦点为顶点，顶点为焦点的双曲线方程是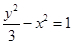
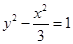
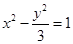
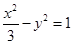
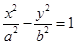的一条渐近线方程为
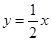，则该双曲线的离心率为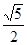
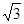
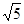
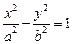（a＞0，b＞0）的右焦点为F，O为坐标原点．若以F为圆心，FO为半径的圆与双曲线C的一条渐近线交于点A（不同于O点），则△OAF的面积为 
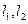，经
过右焦点F垂直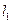
的直线分别交
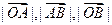成等差数列，且
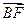与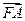
同向，则双曲线的离心率 .
的焦点为焦点，离心率为2的双曲线方程为 。