题目内容
在慈利县工业园区有相距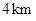 的
的 ,
, 两点,要围垦出以
两点,要围垦出以 为一条对角线的平行四边形区域建制造厂。按照规划,围墙总长为
为一条对角线的平行四边形区域建制造厂。按照规划,围墙总长为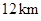 .在设计图纸上,建立平面直角坐标系如图(
.在设计图纸上,建立平面直角坐标系如图(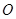 为
为 的中点),那么平行四边形另外两个顶点
的中点),那么平行四边形另外两个顶点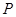 ,
,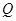 的坐标满足的方程是
的坐标满足的方程是
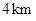 的
的 ,
, 两点,要围垦出以
两点,要围垦出以 为一条对角线的平行四边形区域建制造厂。按照规划,围墙总长为
为一条对角线的平行四边形区域建制造厂。按照规划,围墙总长为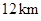 .在设计图纸上,建立平面直角坐标系如图(
.在设计图纸上,建立平面直角坐标系如图( 为
为 的中点),那么平行四边形另外两个顶点
的中点),那么平行四边形另外两个顶点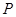 ,
,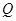 的坐标满足的方程是
的坐标满足的方程是
A. | B.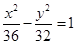 | C. | D.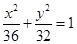 |
C
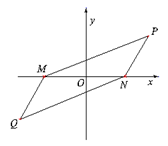
分析:由题意可得 PM+PN=6>MN=4,故点P的轨迹是以M,N为焦点的椭圆,且a=3,c=2,∴b= 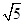 ,
,
求得点P的轨迹方程,从而得到结论.
解答:解:由题意可得 PM+PN=6>MN=4,故点P的轨迹是以M,N为焦点的椭圆,且a=3,c=2,∴b=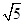 ,
,
故椭圆的方程为 . 同理,点Q的轨迹也是此椭圆,
. 同理,点Q的轨迹也是此椭圆,
故选 C.
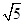 ,
,求得点P的轨迹方程,从而得到结论.
解答:解:由题意可得 PM+PN=6>MN=4,故点P的轨迹是以M,N为焦点的椭圆,且a=3,c=2,∴b=
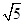 ,
,故椭圆的方程为
 . 同理,点Q的轨迹也是此椭圆,
. 同理,点Q的轨迹也是此椭圆,故选 C.

练习册系列答案
相关题目
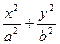 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为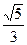 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.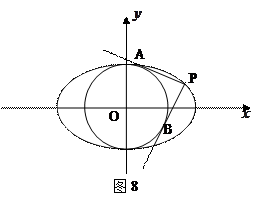
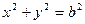 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.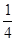
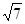 B、8, 6,
B、8, 6, 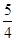 D、4, 3,
D、4, 3, 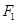 、
、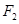 是离心率为
是离心率为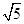 的双曲线
的双曲线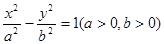 的左、右两个焦点,若双曲线右支上存在一点P,使
的左、右两个焦点,若双曲线右支上存在一点P,使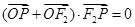 (O为坐标原点)且
(O为坐标原点)且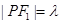
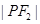 则
则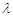 的值为
的值为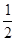
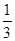
 的焦点坐标是( )
的焦点坐标是( )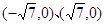
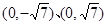
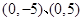
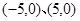
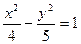 右支上一点
右支上一点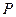 到左焦
到左焦 点的距离为
点的距离为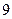 ,则
,则 ( )
( ) 
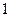

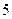
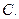

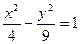 的渐近线方程是
的渐近线方程是 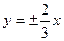
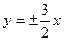
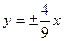
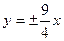
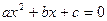 无实根,则双曲线
无实根,则双曲线 的离心率的取值范围为.
的离心率的取值范围为.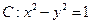 的渐近线方程为_____; 若双曲线
的渐近线方程为_____; 若双曲线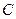 的右顶点为
的右顶点为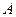 ,过
,过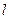 与双曲线
与双曲线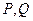 两点,且
两点,且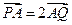 ,则直线
,则直线