题目内容
已知各项均为正数的等比数列{an}的首项a1=2,Sn为其前n项和,若5S1,S3,3S2成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an,cn= ,记数列{cn}的前n项和Tn.若对?n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.
,记数列{cn}的前n项和Tn.若对?n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.
(1)求数列{an}的通项公式;
(2)设bn=log2an,cn=
 ,记数列{cn}的前n项和Tn.若对?n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.
,记数列{cn}的前n项和Tn.若对?n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.(1)an=2n(2)

(1)设数列{an}的公比为q,∵5S1,S3,3S2成等差数列,
∴2S3=5S1+3S2,即2(a1+a1q+a1q2)=5a1+3(a1+a1q),
化简得2q2-q-6=0,解得q=2或q=- .
.
因为数列{an}的各项均为正数,所以q=- 不合题意,
不合题意,
所以数列{an}的通项公式为an=2n.
(2)由bn=log2an得bn=log22n=n,
则cn= =
= =
= -
- ,
,
Tn=1-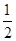 +
+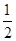 -
-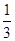 +…+
+…+ -
- =1-
=1- =
= .
.
∵ ≤k(n+4),∴k≥
≤k(n+4),∴k≥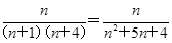 =
=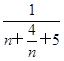 .
.
∵n+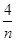 +5≥2
+5≥2 +5=9,当且仅当n=
+5=9,当且仅当n=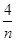 ,即n=2时等号成立,
,即n=2时等号成立,
∴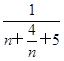 ≤
≤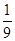 ,因此k≥
,因此k≥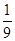 ,故实数k的取值范围为
,故实数k的取值范围为
∴2S3=5S1+3S2,即2(a1+a1q+a1q2)=5a1+3(a1+a1q),
化简得2q2-q-6=0,解得q=2或q=-
 .
.因为数列{an}的各项均为正数,所以q=-
 不合题意,
不合题意,所以数列{an}的通项公式为an=2n.
(2)由bn=log2an得bn=log22n=n,
则cn=
 =
= =
= -
- ,
,Tn=1-
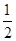 +
+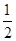 -
-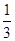 +…+
+…+ -
- =1-
=1- =
= .
.∵
 ≤k(n+4),∴k≥
≤k(n+4),∴k≥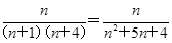 =
=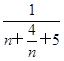 .
.∵n+
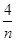 +5≥2
+5≥2 +5=9,当且仅当n=
+5=9,当且仅当n=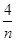 ,即n=2时等号成立,
,即n=2时等号成立,∴
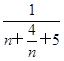 ≤
≤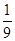 ,因此k≥
,因此k≥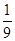 ,故实数k的取值范围为
,故实数k的取值范围为

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.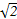 )
)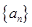 满足
满足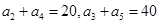 ,则前
,则前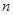 项
项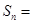 ___ __.
___ __.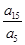 =( ).
=( ).