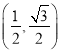Question

【题目】如图，长方体ABCD﹣A1B1C1D1中，AB=AD=1，AA1=2，点P为DD1的中点．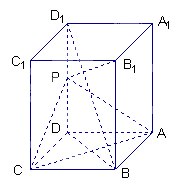
（1）求证：直线BD1∥平面PAC；
（2）求证：直线PB1⊥平面PAC．
（3）求三棱锥B﹣PAC的体积．

Answer 1

【答案】
（1）证明：设AC和BD交于点O，连PO，

由P，O分别是DD1，BD的中点，故PO∥BD1，

所以直线BD1∥平面PAC

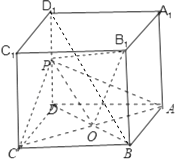
（2）证明：PC2=2，PB12=3，B1C2=5，所以△PB1C是直角三角形．

所以PB1⊥PC，

同理PB1⊥PA，所以直线PB1⊥平面PAC

（3）解：因为P为中点，所以PD=1，易知△ABC为直角三角形，且AB=BC=1，

所以

【解析】（1）直接利用三角形的中位线，得到线线平行，进一步利用线面平行的判定定理得到结论．（2）利用线面垂直的判定和性质定理和勾股定理得逆定理得到线线垂直，进一步利用线面垂直的判定得到结论．（3）利用等体积法，求三棱锥B﹣PAC的体积．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对平面与平面垂直的判定的理解，了解一个平面过另一个平面的垂线，则这两个平面垂直．