题目内容
【题目】设在平面上有两个向量a=(cos 2α,sin 2α)(0≤α<π),b=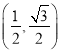 ,a与b不共线.
,a与b不共线.
(1)求证:向量a+b与a-b垂直;
(2)当向量![]() a+b与a-
a+b与a-![]() b的模相等时,求α的大小.
b的模相等时,求α的大小.
【答案】(1)见解析;(2)α=![]() 或α=
或α=![]() .
.
【解析】试题分析:(1)计算![]() ,
, ![]() ,利用(
,利用(![]() +
+![]() )·(
)·(![]() -
-![]() )=0即可证得垂直;
)=0即可证得垂直;
(2)由|![]() +
+![]() |=|
|=|![]() -
-![]() |两边平方,得3|
|两边平方,得3|![]() |2+2
|2+2![]() ·
·![]() +|
+|![]() |2=|
|2=|![]() |2-2
|2-2![]() ·
·![]() +3|
+3|![]() |2,,得sin
|2,,得sin![]() =0,即可求角.
=0,即可求角.
试题解析:
(1)由已知得![]() =
=![]() =1,
=1, ![]() =
= =1,
=1,
则(![]() +
+![]() )·(
)·(![]() -
-![]() )=
)=![]() 2-
2-![]() 2=0,
2=0,
所以![]() +
+![]() 与a-
与a-![]() 垂直.
垂直.
(2)由|![]() +
+![]() |=|
|=|![]() -
-![]() |两边平方,得3|
|两边平方,得3|![]() |2+2
|2+2![]() ·
·![]() +|
+|![]() |2=|
|2=|![]() |2-2
|2-2![]() ·
·![]() +3|
+3|![]() |2,
|2,
∴2(|![]() |2-|
|2-|![]() |2)+4
|2)+4![]() ·
·![]() =0.
=0.
而|![]() |=|
|=|![]() |,∴
|,∴![]() ·
·![]() =0.
=0.
∴![]() cos 2α+
cos 2α+![]() sin 2α=0,即sin
sin 2α=0,即sin![]() =0,
=0,
∴2α+![]() =kπ(k∈Z).
=kπ(k∈Z).
又0≤α<π,∴α=![]() 或α=
或α=![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目