题目内容
【题目】已知动圆过定点![]() ,且在
,且在![]() 轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.
轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.
(Ⅰ)求直线![]() 与曲线C围成的区域面积;
与曲线C围成的区域面积;
(Ⅱ)点![]() 在直线
在直线![]() 上,点
上,点![]() ,过点
,过点![]() 作曲线C的切线
作曲线C的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
【答案】(Ⅰ) ![]() (Ⅱ)1
(Ⅱ)1
【解析】试题分析:可出设动圆圆心的坐标为![]() ,根据题设用直接法可得曲线方程;(Ⅰ)直线方程和曲线方程联立求交点坐标,根据定积分求曲边形面积可得结果;(Ⅱ)设
,根据题设用直接法可得曲线方程;(Ⅰ)直线方程和曲线方程联立求交点坐标,根据定积分求曲边形面积可得结果;(Ⅱ)设![]() 、
、![]() ,
, ![]() ,根据导数求切线斜率,设切线方程,由韦达定理
,根据导数求切线斜率,设切线方程,由韦达定理![]() 、
、![]() 用
用![]() ,表示可得
,表示可得![]() .
.
试题解析:(Ⅰ)设动圆圆心的坐标为![]() ,由题意可得,
,由题意可得, ![]() ,化简得
,化简得![]() , 联立方程组
, 联立方程组![]() ,解得
,解得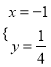 或
或![]() ,所以直线
,所以直线![]() 与曲线C围成的区域面积为
与曲线C围成的区域面积为![]() ;
;
(Ⅱ)设![]() 、
、![]() ,则由题意可得,切线
,则由题意可得,切线![]() 的方程为
的方程为![]() ,切线
,切线![]() 的方程为
的方程为![]() ,再设点
,再设点![]() ,从而有
,从而有 ,所以可得出直线AB的方程为
,所以可得出直线AB的方程为![]() ,即
,即![]() .
.
联立方程组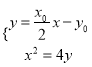 ,得
,得![]() ,又
,又![]() ,所以有
,所以有![]() ,
,
可得![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() ,
,
所以常数![]() .
.
【方法点晴】本题主要考查抛物线标准方程、定积分的应用以及解析几何中的存在性问题,属于难题.解决存在性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在,注意:①当条件和结论不唯一时要分类讨论;②当给出结论而要推导出存在的条件时,先假设成立,再推出条件;③当条件和结论都不知,按常规方法题很难时采取另外的途径.

练习册系列答案
相关题目