题目内容
【题目】已知椭圆方程![]() ,其左焦点、上顶点和左顶点分别为
,其左焦点、上顶点和左顶点分别为![]() ,
, ![]() ,
, ![]() ,坐标原点为
,坐标原点为![]() ,且线段
,且线段![]() ,
, ![]() ,
, ![]() 的长度成等差数列.
的长度成等差数列.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若过点![]() 的一条直线
的一条直线![]() 交椭圆于点
交椭圆于点![]() ,
, ![]() ,交
,交![]() 轴于点
轴于点![]() ,使得线段
,使得线段![]() 被点
被点![]() ,
, ![]() 三等分,求直线
三等分,求直线![]() 的斜率.
的斜率.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]() .
.
【解析】试题分析: (Ⅰ)由线段![]() ,
, ![]() ,
, ![]() 的长度成等差数列,以及
的长度成等差数列,以及![]() ,可求得离心率; (Ⅱ)设直线
,可求得离心率; (Ⅱ)设直线![]() 的方程为
的方程为![]() ,先研究
,先研究![]() 的情况,根据
的情况,根据![]() ,求出
,求出![]() 将直线
将直线![]() 的方程和椭圆方程联立求出点
的方程和椭圆方程联立求出点![]() 的横坐标,根据对称性可知直线
的横坐标,根据对称性可知直线![]() 的斜率.
的斜率.
试题解析:(Ⅰ)依题意有![]() ,
,
把上式移项平方并把![]() ,代入得
,代入得![]() ,
,
所以椭圆的离心率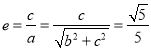 .
.
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,先研究
,先研究![]() 的情况,要使
的情况,要使![]() ,
,
则![]() ,
, ![]() ,
,
因此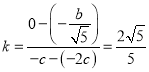 .
.
将直线![]() 的方程和椭圆方程联立可得
的方程和椭圆方程联立可得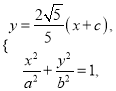 解得
解得![]()
由于点![]() 的横坐标为
的横坐标为![]() ,因此
,因此![]() 也等于
也等于![]() ,
,
由对称性可知直线![]() 的斜率为
的斜率为![]() 或
或![]() .
.

练习册系列答案
相关题目