题目内容
13.平面上三个力$\overrightarrow{{F}_{1}}$,$\overrightarrow{{F}_{2}}$,$\overrightarrow{{F}_{3}}$作用于一点且处于平衡状态,已知|$\overrightarrow{{F}_{1}}$|=1N,|$\overrightarrow{{F}_{2}}$|=2N,$\overrightarrow{{F}_{1}}$,$\overrightarrow{{F}_{2}}$成120°角,则力$\overrightarrow{{F}_{1}}$与$\overrightarrow{{F}_{3}}$所成的角为90°.分析 如图所示,A(1,0),∠AOB=120°.$\overrightarrow{OA}=\overrightarrow{{F}_{1}}$,$\overrightarrow{OB}$=$\overrightarrow{{F}_{2}}$.把$\overrightarrow{OB}$=$\overrightarrow{{F}_{2}}$.分别沿x,y轴方向正交分解,可得$\overrightarrow{OD}$.由于三个力$\overrightarrow{{F}_{1}}$,$\overrightarrow{{F}_{2}}$,$\overrightarrow{{F}_{3}}$作用于一点且处于平衡状态,即$\overrightarrow{{F}_{1}}+\overrightarrow{{F}_{2}}$+$\overrightarrow{{F}_{3}}$=$\overrightarrow{0}$,可得$\overrightarrow{{F}_{3}}=-\overrightarrow{OD}$,即可得出.
解答 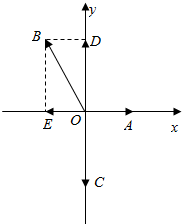 解:如图所示,
解:如图所示,
A(1,0),∠AOB=120°.
$\overrightarrow{OA}=\overrightarrow{{F}_{1}}$,$\overrightarrow{OB}$=$\overrightarrow{{F}_{2}}$.
把$\overrightarrow{OB}$=$\overrightarrow{{F}_{2}}$.分别沿x,y轴方向正交分解,
可得$\overrightarrow{OD}$=$(0,\sqrt{3})$.
∵三个力$\overrightarrow{{F}_{1}}$,$\overrightarrow{{F}_{2}}$,$\overrightarrow{{F}_{3}}$作用于一点且处于平衡状态,
∴$\overrightarrow{{F}_{1}}+\overrightarrow{{F}_{2}}$+$\overrightarrow{{F}_{3}}$=$\overrightarrow{0}$,
∴$\overrightarrow{{F}_{3}}=-\overrightarrow{OD}$=-(0,$\sqrt{3}$)=$(0,-\sqrt{3})$.
∴力$\overrightarrow{{F}_{1}}$与$\overrightarrow{{F}_{3}}$所成的角为90°.
故答案为:90°.
点评 本题考查了向量的正交分解、向量的运算性质,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (-$\frac{1}{2}$,+∞) | B. | (-∞,-$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$] | D. | [-$\frac{1}{2}$,+∞) |
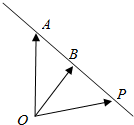 如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )
如图,设一条直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面上任意一点,则( )| A. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}+λ\overrightarrow{OB}}{1+λ}$(λ≠-1) | B. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}+λ\overrightarrow{OB}}{1-λ}$ | ||
| C. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}-λ\overrightarrow{OB}}{1+λ}$(λ≠-1) | D. | $\overrightarrow{OP}$=$\frac{\overrightarrow{OA}-2λ\overrightarrow{OB}}{1-λ}$ |
 执行如图所示的程序框图,运行的结果是4,则输入的x的值可以是( )
执行如图所示的程序框图,运行的结果是4,则输入的x的值可以是( )| A. | 2,4或16 | B. | -2,2或4 | C. | -2,2或16 | D. | -2,4或16 |
| A. | {x|x<2ab或x≥a2+b2} | B. | {x|x≤2ab或x≥a2+b2} | C. | {x|x<2ab或x>a2+b2} | D. | {x|2ab<x≤a2+b2} |
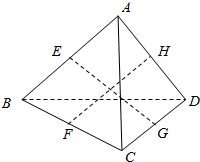 如图所示.已知E、F、G、H分别是四边形ABCD各边的中点.若EG⊥FH,求证:AC=BD.
如图所示.已知E、F、G、H分别是四边形ABCD各边的中点.若EG⊥FH,求证:AC=BD.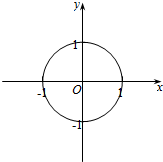 借助单位圆求sinx=$\frac{1}{2}$时,x的值?
借助单位圆求sinx=$\frac{1}{2}$时,x的值?