Question

8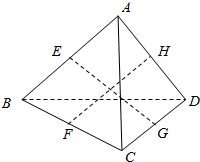．如图所示．已知E、F、G、H分别是四边形ABCD各边的中点．若EG⊥FH，求证：AC=BD．

Answer 1

分析 根据三角形中位线定理，可得EF∥AC∥HG，EH∥BD∥FG，进而得到四边形EFGH为平行四边形，再由对角线互相垂直，得到四边形EFGH为菱形，进而得到答案．

解答 证明：∵E、F、G、H分别是四边形ABCD各边的中点．
∴EF∥AC∥HG，EH∥BD∥FG，
故四边形EFGH为平行四边形，
又∵EG⊥FH，
故四边形EFGH为菱形，
∴EF=FG．
又∵EF=$\frac{1}{2}$AC，FG=$\frac{1}{2}$BD．
∴AC=BD．

点评 本题考查的知识点是三角形中位线定理，平行四边形的判定与性质，菱形的判定与性质，难度中档．