题目内容
18.已知:x∈(0,+∞),观察下列式子:x+$\frac{1}{x}≥2,x+\frac{4}{x^2}=\frac{x}{2}+\frac{x}{2}+\frac{4}{x^2}$≥3…类比有x+$\frac{a}{x^n}≥n+1({n∈{N^*}})$,则a的值为nn.分析 根据已知中x∈(0,+∞),观察下列式子:x+$\frac{1}{x}≥2,x+\frac{4}{x^2}=\frac{x}{2}+\frac{x}{2}+\frac{4}{x^2}$≥3…归纳可得:x+$\frac{{n}^{2}}{{x}^{n}}≥n+1(n∈{N}^{*})$,进而得到答案.
解答 解:由已知中:x∈(0,+∞)时,
x+$\frac{1}{x}≥2,x+\frac{4}{x^2}=\frac{x}{2}+\frac{x}{2}+\frac{4}{x^2}$≥3,
…
归纳推理得:x+$\frac{{n}^{2}}{{x}^{n}}≥n+1(n∈{N}^{*})$,
故a=nn,
故答案为:nn
点评 本题考查归纳推理,解题的关键在于发现左式中的规律,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
13.已知$\frac{\overline z}{i}$=2-i,则在复平面内,复数z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知命题p对任意x∈R,总有|x-1|+|x+1|>2;命题q:x>2是x>1的充分不必要条件.则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧¬q | C. | ¬p∧q | D. | p∧¬q |
 砷是广泛分布于自然界中的非金属元素,长期饮用高砷水会直接危害群众的身心健康和生命安全,而近水农村地区,水质情况更需要关注.为了解甲、乙两地区农村居民饮用水中砷含量的基本情况,分别在两地随机选取10个村子,其砷含量的调查数据如下(单位:mg/1000L):
砷是广泛分布于自然界中的非金属元素,长期饮用高砷水会直接危害群众的身心健康和生命安全,而近水农村地区,水质情况更需要关注.为了解甲、乙两地区农村居民饮用水中砷含量的基本情况,分别在两地随机选取10个村子,其砷含量的调查数据如下(单位:mg/1000L):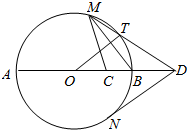 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.