题目内容
6.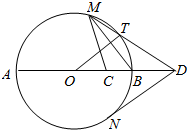 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.(Ⅰ)求证:DT•DM=DO•DC;
(Ⅱ)若∠DOT=30°,求∠BMC.
分析 (1)可证△DCN与△DNO相似,得DN2=DB•DO,由切割线定理可得DN2=DT•DM,即可得证;
(2)结合(1)的结论证得△DTO∽△DCM,得到两个角∠DOT、∠DMC相等,结合圆周角定理即可求得∠BMC.
解答 (Ⅰ)证明:连接ON,∠OND=90°,$BN=\frac{1}{2}OD=OB=ON$,△OBN为等边三角形,则CN⊥OB,
可证△DCN与△DNO相似,得DN2=DB•DO;
又DN2=DT•DM,则DT•DM=DO•DC-------(5分)
(Ⅱ)解:由(Ⅰ)知,$\frac{DT}{DC}=\frac{DO}{DM}$,且∠TDO=∠CDM,
所以△DTO与△DBM相似,则∠DOT=∠DMC-------(10分)
因为$∠BMT=\frac{1}{2}∠BOT={15°}$,所以∠BMC=15°
点评 本题主要考查与圆有关的比例线段、圆中的切割线定理以及相似三角形,属于基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
17.直线l 交椭圆$\frac{x^2}{8}+\frac{y^2}{4}$=1于M、N两点,椭圆的上顶点为B点,若△BMN的重心恰好落在椭圆的右焦点上,则直线l的方程是( )
| A. | 2x-3y-9=0 | B. | 3x-2y-11=0 | C. | 3x+2y-7=0 | D. | x-y-5=0 |
1.在一次跳伞训练中,甲、乙两位学员各跳一次,设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员降落在指定范围”可表示为( )
| A. | (¬p)∨(¬p) | B. | ¬((¬p)∧(¬p)) | C. | (¬p)∧(¬p) | D. | ¬(p∨p) |
13.甲乙两位同学最近五次模考数学成绩茎叶图如图,则平均分数较高和成绩比较稳定的分别是( )
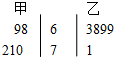
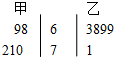
| A. | 甲、甲 | B. | 乙、甲 | C. | 甲、乙 | D. | 乙、乙 |
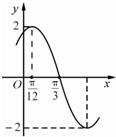 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.