题目内容
已知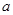 、
、 为异面直线,点A、B在直线
为异面直线,点A、B在直线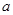 上,点C、D在直线
上,点C、D在直线 上,且AC=AD,BC=BD,则直线
上,且AC=AD,BC=BD,则直线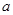 、
、 所成的角为 ( )
所成的角为 ( )
A. 900 B. 600 C. 450 D. 300
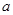 、
、 为异面直线,点A、B在直线
为异面直线,点A、B在直线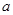 上,点C、D在直线
上,点C、D在直线 上,且AC=AD,BC=BD,则直线
上,且AC=AD,BC=BD,则直线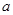 、
、 所成的角为 ( )
所成的角为 ( )A. 900 B. 600 C. 450 D. 300
A
试题分析:取CD中点E,连结AE、BE,因为AC=AD,BC=BD,故CD
 AE,CD
AE,CD BE,可得CD
BE,可得CD 平面ABE,又
平面ABE,又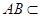 平面ABE,所以CD
平面ABE,所以CD AB,即直线
AB,即直线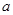 、
、 所成的角为
所成的角为 ,选A.
,选A.
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD,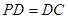 ,E是PC的中点.
,E是PC的中点.
 平面EDB;
平面EDB; ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
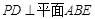 ;
; 的平面角的正弦值.
的平面角的正弦值. 的正方形
的正方形 中,
中, 分别为
分别为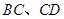 的中点,
的中点, 分别为
分别为 的中点,现沿
的中点,现沿 折叠,使
折叠,使 三点重合,重合后的点记为
三点重合,重合后的点记为 ,构成一个三棱锥.
,构成一个三棱锥.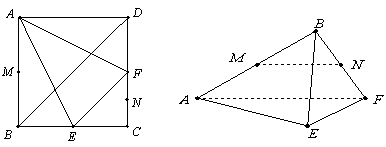
 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明; 平面
平面 ;
; 的体积.
的体积.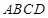 -
-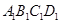 ,
, =2,
=2,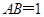 ,
,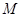 ,
,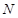 分别在
分别在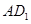 ,
,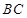 上移动,且始终保持
上移动,且始终保持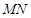 ∥平面
∥平面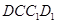 ,设
,设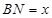 ,
,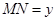 ,则函数
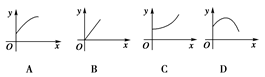
,则函数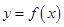 的图象大致是( )
的图象大致是( )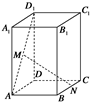

 ,两个平面
,两个平面 .下面四个命题中不正确的是( )
.下面四个命题中不正确的是( )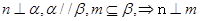
 ,
, ,
, ;
;
 ,
,



 是两条不同直线,
是两条不同直线, 是两个不同的平面,下列命题正确的是( )
是两个不同的平面,下列命题正确的是( ) 且
且 则
则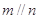
 且
且 ,则
,则
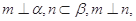 则
则 则
则