题目内容
16.(Ⅰ)已知0<α<π,sin αcos α=-$\frac{60}{169}$,求sinα-cosα的值;(Ⅱ)已知sinθ+cosθ=m,求sin3θ+cos3θ的值.
分析 (Ⅰ)由0<α<π,sinαcosα的值小于,判断得到sinα-cosα的值为正数,利用完全平方公式及同角三角函数基本关系求出sinα-cosα的值即可;
(Ⅱ)把已知等式两边平方求出sinθcosθ的值,原式利用立方和公式变形,将各自的值代入计算即可求出值.
解答 解:(Ⅰ)∵0<α<π,sinαcosα=-$\frac{60}{169}$,
∴sinα>0,cosα<0,即sinα-cosα>0,
∴(sinα-cosα)2=1-2sinαcosα=$\frac{289}{169}$,
则sinα-cosα=$\frac{17}{13}$;
(Ⅱ)∵sinθ+cosθ=m,
∴(sinθ+cosθ)2=1+2sinθcosθ=m2,即sinθcosθ=$\frac{{m}^{2}-1}{2}$,
则原式=(sinθ+cosθ)(sin2θ+cos2θ-sinθcosθ)=(sinθ+cosθ)(1-sinθcosθ)=m(1-$\frac{{m}^{2}-1}{2}$)=$\frac{3m-{m}^{3}}{2}$.
点评 此题考查了同角三角函数基本关系的应用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
7.如图所示,平面内z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,则|z1+z2|=( )
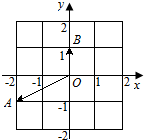

| A. | 2 | B. | 3 | C. | 2 $\sqrt{2}$ | D. | 3 $\sqrt{3}$ |
4.已知集合M={x|0<x<3},N={x|log2x>1},则M∩N=( )
| A. | ∅ | B. | {x|0<x<3} | C. | {x|1<x<3} | D. | {x|2<x<3} |
11.在(2x2-x-1)5的二项展开式中,x的系数为( )
| A. | 10 | B. | -10 | C. | 40 | D. | -40 |
5.如果数列{an}中,满足a1,$\frac{{a}_{2}}{{a}_{1}}$,$\frac{{a}_{3}}{{a}_{2}}$,…,$\frac{{a}_{n}}{{a}_{n-1}}$是首项为1公比为3的等比数列,则a100等于( )
| A. | 3100 | B. | 390 | C. | 34950 | D. | 35050 |
6.在△ABC中,已知A是三角形的内角,且sinA+cosA=$\frac{3}{5}$,则△ABC一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 无法确定三角形的形状 |
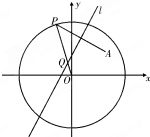 如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )
如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )