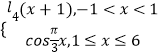题目内容
【题目】选修4-4:坐标系与参数方程
已知直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() ,圆
,圆![]() 的极坐标方程
的极坐标方程![]() .
.
(1)写出直线![]() 的参数方程,并把圆
的参数方程,并把圆![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)设圆![]() 上的点
上的点![]() 到直线
到直线![]() 的距离最近,点
的距离最近,点![]() 到直线
到直线![]() 的距离最远,求点
的距离最远,求点![]() 的横坐标之积.
的横坐标之积.
【答案】(1) 圆![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2) 点
;(2) 点![]() 的横坐标之积为
的横坐标之积为![]() .
.
【解析】试题分析:(I)由题意可得直线l的参数方程为: 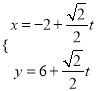 (t为参数).圆C的极坐标方程是ρ=2cosθ即ρ2=2ρcosθ,利用ρ2=x2+y2,x=ρcosθ即可化为直角坐标方程.
(t为参数).圆C的极坐标方程是ρ=2cosθ即ρ2=2ρcosθ,利用ρ2=x2+y2,x=ρcosθ即可化为直角坐标方程.
(II)经过圆心(1,0)且与直线l垂直的直线方程为:y=﹣(x﹣1),即直线AB的方程.与圆的方程联立化为: ![]() .利用根与系数的关系即可得出.
.利用根与系数的关系即可得出.
试题解析:
(1)直线![]() 的参数方程为
的参数方程为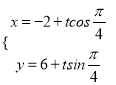 即
即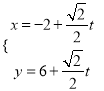 (
(![]() 为参数)
为参数)
由![]() 得
得![]()
因为![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,即圆
,即圆![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)将直线![]() 的参数方程化为直角坐标方程是
的参数方程化为直角坐标方程是![]() ,
,
过圆心![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,
即![]() .
.
则直线![]() :
: ![]() 与圆
与圆![]() :
: ![]() 的交点为
的交点为![]() 两点.
两点.
设点![]() 的横坐标分别为
的横坐标分别为![]() ,联立
,联立![]() 消去
消去![]() ,
,
得![]() ,则
,则![]() .
.
故点![]() 的横坐标之积为
的横坐标之积为![]() .
.

练习册系列答案
相关题目