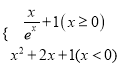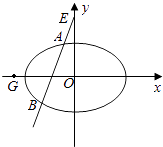题目内容
【题目】已知直线： 
ax+by=1（其中a，b是实数） 与圆：x2+y2=1（O是坐标原点）相交于A，B两点，且△AOB是直角三角形，点P（a，b）是以点M（0，1）为圆心的圆M上的任意一点，则圆M的面积最小值为 ．
【答案】（3﹣2 
）π
【解析】解：由圆x2+y2=1，所以圆心（0，0），半径为1所以|OA|=|OB|=1，则△AOB是等腰直角三角形，得到|AB|=
则圆心（0，0）到直线 ax+by=1的距离为 
，
所以2a2+b2=2，即a2+ 
=1．
因此，圆M的面积最小时，所求半径为椭圆a2+ =1上点P（a，b）到焦点（0，1）的距离最小值，由椭圆的性质，可知最小值为 ﹣1．
所以圆M的面积最小值为π（ ﹣1）2=（3﹣2 ）π．
所以答案是：（3﹣2 ）π．
练习册系列答案
一本好题口算题卡系列答案
相关题目
