Question

【题目】已知平面α与平面β相交于直线l，l1在平面α内，l2在平面β内，若直线l1和l2是异面直线，则下列说法正确的是（ ）
A.l与都相交l1 ， l2
B.l至少与l1 ， l2中的一条相交
C.l至多与l1 ， l2中的一条相交
D.l与l1 ， l2都不相交

Answer 1

【答案】B
【解析】解：A．l可以和l1 ， l2都相交，如下图： ，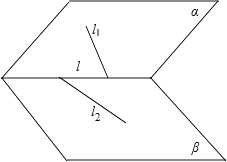
∴该选项错误；
B．“l至少与l1 ， l2中的一条相交”正确，假如l和l1 ， l2都不相交；
∵l和l1 ， l2都共面；
∴l和l1 ， l2都平行；
∴l1∥l2 ， l1和l2共面，这样便不符合已知的l1和l2异面；
∴该选项正确．
C．l与l1 ， l2可以相交，如图：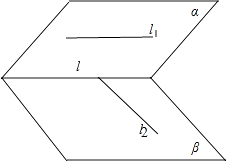

∴该选项错误；
D．l可以和l1 ， l2中的一个平行，如上图，∴该选项错误；
故选：B．
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案，需要熟知相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．