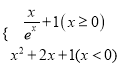题目内容
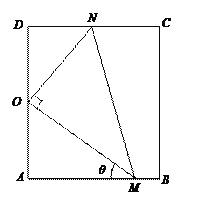
【题目】如图,矩形ABCD是某小区户外活动空地的平面示意图,其中AB=50![]() 米,AD=100米,现拟在直角三角形OMN内栽植草坪供儿童踢球娱乐(其中,点O为AD的中点,OM⊥ON,点M在AB上,点N在CD上),将破旧的道路AM重新铺设.已知草坪成本为每平方米20元,新道路AM成本为每米500元,设∠OMA=θ,记草坪栽植与新道路铺设所需的总费用为f(θ).
米,AD=100米,现拟在直角三角形OMN内栽植草坪供儿童踢球娱乐(其中,点O为AD的中点,OM⊥ON,点M在AB上,点N在CD上),将破旧的道路AM重新铺设.已知草坪成本为每平方米20元,新道路AM成本为每米500元,设∠OMA=θ,记草坪栽植与新道路铺设所需的总费用为f(θ).
(1)求f(θ)关于θ函数关系式,并写出定义域;
(2)为节约投入成本,当tanθ为何值时,总费用 f(θ)最小?
【答案】(1)f(θ)=![]() ,其定义域为
,其定义域为![]() ;(2)
;(2)![]()
【解析】试题分析:(1)在RtOAM中,解出![]() ,在RtODN中求出ON=
,在RtODN中求出ON=![]() ,故可得
,故可得![]() ,由题意当点M与点B重合时,θ取最小值
,由题意当点M与点B重合时,θ取最小值![]() ;当点N与点C重合时,θ取最大值
;当点N与点C重合时,θ取最大值![]() ,即
,即![]() ,故可得最后结果;(2)由(1)可得
,故可得最后结果;(2)由(1)可得![]() ,对其求导,利用导数判断其单调性得其最值.
,对其求导,利用导数判断其单调性得其最值.
试题解析:(1)据题意,在RtOAM中,OA=50,∠OMA=θ,所以AM=![]() ,OM=
,OM=![]() ,据平面几何知识可知∠DON=θ,在RtODN中,OD=50,∠DON=θ,所以ON=
,据平面几何知识可知∠DON=θ,在RtODN中,OD=50,∠DON=θ,所以ON=![]() ,所以f(θ)=
,所以f(θ)=![]() =
=![]() =
=![]() ,据题意,当点M与点B重合时,θ取最小值
,据题意,当点M与点B重合时,θ取最小值![]() ;当点N与点C重合时,θ取最大值
;当点N与点C重合时,θ取最大值![]() ,所以
,所以![]() ,所以f(θ)=
,所以f(θ)=![]() ,其定义域为
,其定义域为![]() .
.
(2)由(1)可知,f(θ)=![]() ,
, ![]() ,
, ![]() =
=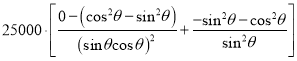 =
=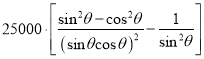 =
=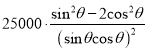 ,
,
令![]() =0,得
=0,得![]() ,其中
,其中![]() ,列表:
,列表:
θ |
|
|
|
|
|
|
|
|
| ||
|
| ↘ | 极小值 | ↗ |
|
所以当![]() 时,总费用 f(θ)取最小值
时,总费用 f(θ)取最小值![]() ,可节约投入成本.
,可节约投入成本.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目