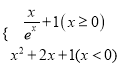题目内容
【题目】已知函数y=x+ 
（a＞0）在区间 
上单调递减，在区间 
上单调递增；函数 
（1）请写出函数f（x）=x2+ 
（a＞0）与函数g（x）=xn+ 
（a＞0，n∈N，n≥3）在（0，+∞）的单调区间（只写结论，不证明）；
（2）求函数h（x）的最值；
（3）讨论方程h2（x）﹣3mh（x）+2m2=0（0＜m≤30）实根的个数．
【答案】
（1）解：根据条件， 
的单调递减区间是 
，
单调递增区间是 
；
函数 
的单调递减区间是 
，单调递增区间是 
（2）解： 
= 
由（1）可知， 
与 
均在 
单调递减，在[1，2]上单调递增，
则有函数h（x）在 单调递减，在[1，2]上单调递增，
所以 
， 
（3）解：由h2（x）﹣3mh（x）+2m2=0可得（h（x）﹣m）（h（x）﹣2m）=0，
所以有h（x）=m或h（x）=2m，
又函数h（x）在 单调递减，在[1，2]单调递增，
而 
，
所以当0＜2m＜160＜m＜8时，方程无实数根；
当2m=16m=8时，有一个实数根；
当0＜m＜16，且60＞2m＞16即8＜m＜16，方程有两个实数根；
当m=16，2m=32，方程有三个实数根；
当 
时，方程有四个实数根．
综上，①当0＜m＜8时，方程实根个数为0；
②当m=8时，方程实根个数为1；
③当8＜m＜16时，方程实根个数为2；
④当m=16，2m=32时，方程实根个数为3；
⑤当16＜m≤30时，方程实根个数为4
【解析】（1）由已知函数y=x+ 
的单调区间，即可得到所求函数的单调区间；（2）化简h（x）的函数式，再由已知结论，可得函数h（x）在 单调递减，在[1，2]上单调递增，即可得到所求函数的最值；（3）化简方程可得，h（x）=m或h（x）=2m，又函数h（x）在 单调递减，在[1，2]单调递增，讨论0＜m＜8，m=8，8＜m＜16，16＜m≤30，即可得到方程的根的个数．
【考点精析】关于本题考查的函数的最值及其几何意义，需要了解利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能得出正确答案．
