题目内容
【题目】已知函数f（x）=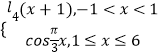 
，若存在实数x1 ， x2 ， x3 ， x4 ， 满足x1＜x2＜x3＜x4 ， 且f（x1）=f（x2）=f（x3）=f（x4），则 
的取值范围是（ ）.
A.（0，4）
B.（0， 
）
C.（ 
， 
）
D.（ 
， 
）
【答案】B
【解析】解：由题意，可得﹣1＜x1＜0＜x2＜1＜x3＜1.5，4.5＜x4＜6， 则|log4（x1+1）|=|log4（x2+1）|，即为﹣log4（x1+1）
=log4（x2+1），
可得（x1+1）（x2+1）=1，
由y=cos 
x的图象关于直线x=3对称，可得x3+x4=6，
则 
=x3x4﹣5=x3（6﹣x3）﹣5=﹣（x3﹣3）2+4在（1，1.5）递增，
即有 的取值范围是（0， 
）．
故选B．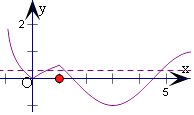
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
