题目内容
20．用一条直线截长方形，可截得一个直角三角形，按图（1）所标边长，得c2=a2+b2．用一个平面截长方体，可截得三棱锥P-ABC，如图（2），若S表示截面面积，S1，S2，S3分别表示其余三个面的面积，则类比得到的结论是S2=S12+S22+S32．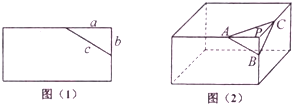
分析 从平面图形到空间图形，模型不变，即可得出结论．
解答 解：建立从平面图形到空间图形的类比，于是作出猜想：S2=S12+S22+S32
故答案为：S2=S12+S22+S32
点评 本题主要考查学生的知识量和知识迁移、类比的基本能力．
练习册系列答案
相关题目
10．如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是（ ）
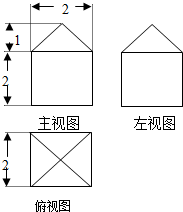
| A． | $（20+4\sqrt{3}）c{m^2}$ | B． | $（20+4\sqrt{2}）c{m^2}$ | C． | $（20+\sqrt{2}）c{m^2}$ | D． | $（10+4\sqrt{2}）c{m^2}$ |
如图所示，已知半圆的直径AB=6cm，CD是半圆上长为2cm的弦，问：当弦CD在半圆上滑动时，AC和BD延长线的夹角是定值吗？若是，试求出这个定角的正弦值；若不是，请说明理由．
12．若M点的极坐标为$（{2，\frac{5π}{6}}）$，则M点的直角坐标是（ ）
| A． | （-$\sqrt{3}$，1） | B． | （-$\sqrt{3}$，-1） | C． | （$\sqrt{3}$，-1） | D． | （$\sqrt{3}$，1） |
9．如图程序图输出的结果是（ ）
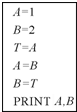
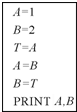
| A． | 2，1 | B． | 2，2 | C． | 1，2 | D． | 1，1 |