题目内容
10.已知函数f(x)=|2x-1|+|2x+a|(a>0)(1)当a=3时,求不等式f(x)≤6的解集;
(2)若关于x的不等式f(x)>2a恒成立,求实数a的取值范围.
分析 (1)当a=3时,不等式即|x-$\frac{1}{2}$|+|x+$\frac{3}{2}$|≤3,再根据绝对值的意义,求得不等式的解集.
(2)利用绝对值三角不等式求得|2x-1|+|2x+a|的最小值为a+1,可得a+1>2a,由此求得a的范围.
解答 解:(1)当a=3时,不等式f(x)≤6,即|2x-1|+|2x+3|≤6,即|x-$\frac{1}{2}$|+|x+$\frac{3}{2}$|≤3.
|x-$\frac{1}{2}$|+|x+$\frac{3}{2}$|表示数轴上的x对应点到-$\frac{3}{2}$、$\frac{1}{2}$对应点的距离之和,而-2和1对应点到-$\frac{3}{2}$、$\frac{1}{2}$对应点的距离之和正好等于3,
故不等式的解集为[-2,1].
(2)因为不等式|2x-1|+|2x+a|>2a恒成立,a>0,而|2x-1|+|2x+a|≥|(2x-1)-(2x+a)|=|a+1|=a+1,
故a+1>2a,求得0<a<1.
点评 本题主要考查绝对值的意义,绝对值三角不等式,绝对值不等式的解法,函数的恒成立问题,体现了转化的数学思想,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
2.函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x-8,x>0}\\{-x-2,x<0}\end{array}\right.$,g(x)=3x-1则使不等式f(g(x))≥0成立的区间为( )
| A. | [1,+∞) | B. | [1n3,+∞) | C. | [1,ln3] | D. | [-1,ln3) |

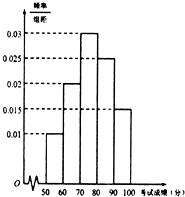 某市为了了解本地高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].
某市为了了解本地高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为[50,60),[60,70),[70,80),[80,90),[90,100].