题目内容
选修4-2:矩阵与变换
设矩阵M=
.
(I)若a=2,b=3,求矩阵M的逆矩阵M-1;
(Ⅱ)若曲线C:x2+4xy+2y2=1在矩阵M的作用下变换成曲线C':x2-2y2=1,求a+b的值.
设矩阵M=
|
(I)若a=2,b=3,求矩阵M的逆矩阵M-1;
(Ⅱ)若曲线C:x2+4xy+2y2=1在矩阵M的作用下变换成曲线C':x2-2y2=1,求a+b的值.
(I)若a=2,b=3,则M=
,∴|M|=
=-5
故所求的逆矩阵M-1=
.…(4分)
(II)设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P'(x',y'),
则
=
,
即
,…(5分)
又点P'(x',y')在曲线C'上,所以x'2-2y'2=1,则(x+ay)2-2(bx+y)2=1,
即(1-2b2)x2+(2a-4b)xy+(a2-2)y2=1为曲线C的方程,
又已知曲线C的方程为x2+4xy+2y2=1,
比较系数可得
,解得b=0,a=2,
∴a+b=2.…(7分)
|
| . |
| . |
故所求的逆矩阵M-1=
|
(II)设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P'(x',y'),
则
|
|
|
即
|
又点P'(x',y')在曲线C'上,所以x'2-2y'2=1,则(x+ay)2-2(bx+y)2=1,
即(1-2b2)x2+(2a-4b)xy+(a2-2)y2=1为曲线C的方程,
又已知曲线C的方程为x2+4xy+2y2=1,
比较系数可得
|
∴a+b=2.…(7分)

练习册系列答案
相关题目
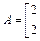
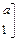 ,a为实数,若点(1,-2)在矩阵A的变换下得到点(-4,0)
,a为实数,若点(1,-2)在矩阵A的变换下得到点(-4,0)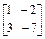 .
.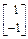 ,试求矩阵X.
,试求矩阵X.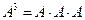 ,若矩阵
,若矩阵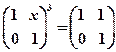 ,则
,则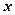 的值是_____________.
的值是_____________.