题目内容
已知矩阵M1=
,矩阵M2表示的是将每个点绕原点逆时针旋转
得到的矩阵,M=M2M1
(Ⅰ)求矩阵M;
(Ⅱ)求矩阵M的特征值及其对应的特征向量.
|
| π |
| 2 |
(Ⅰ)求矩阵M;
(Ⅱ)求矩阵M的特征值及其对应的特征向量.
(Ⅰ)绕原点逆时针旋转90°的变换M2=
.(4分)
∴M=M2M1=
--------(5分)
(Ⅱ)由阵M的特征多项式为f(λ)=
=λ2-3λ-4
令f(λ)=0,得矩阵M的特征值为-1与4.
当λ=-1时,x+y=0,此时的一个特征向量为
;
当λ=4时,2x-3y=0此时的一个特征向量为
.--------(13分)
|
∴M=M2M1=
|
(Ⅱ)由阵M的特征多项式为f(λ)=
| . |
| . |
令f(λ)=0,得矩阵M的特征值为-1与4.
当λ=-1时,x+y=0,此时的一个特征向量为
|
当λ=4时,2x-3y=0此时的一个特征向量为
|

练习册系列答案
相关题目
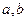 的值;②求
的值;②求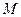 的逆矩阵
的逆矩阵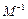
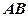 的逆矩阵:
的逆矩阵: 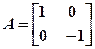 ,
,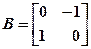 .
. 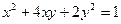 在二阶矩阵
在二阶矩阵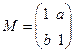 的作用下变换为曲线
的作用下变换为曲线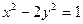
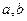 的值;
的值;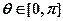 ,且
,且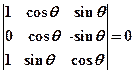 ,则
,则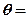 ____________.
____________.