题目内容
已知关于x的方程x2+mx+m+n=0的两根分别为椭圆和双曲线的离心率.记分别以m、n为横纵坐标的点P(m,n)表示的平面区域为D,若函数y=loga(x+3)(a>1)的图象上存在区域D上的点,则实数a的取值范围为( )
| A.a>2 | B.a≥2 | C.1<a<2 | D.1<a≤2 |
构造函数f(x)=x2+mx+m+n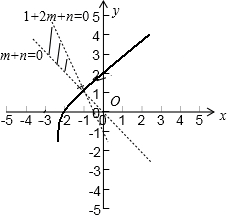
∵关于x的方程x2+mx+m+n=0的两根分别为椭圆和双曲线的离心率
∴方程x2+mx+m+n=0的两根,一根属于(0,1),另一根属于(1,+∞)
∴
,∴
∵直线m+n=0,1+2m+n=0的交点坐标为(-1,1)
∴要使函数y=loga(x+3)(a>1)的图象上存在区域D上的点,则必须满足1<loga(-1+3)
∴loga2>1=logaa,
∵a>1
∴1<a<2
故选C.

∵关于x的方程x2+mx+m+n=0的两根分别为椭圆和双曲线的离心率
∴方程x2+mx+m+n=0的两根,一根属于(0,1),另一根属于(1,+∞)
∴
|
|
∵直线m+n=0,1+2m+n=0的交点坐标为(-1,1)
∴要使函数y=loga(x+3)(a>1)的图象上存在区域D上的点,则必须满足1<loga(-1+3)
∴loga2>1=logaa,
∵a>1
∴1<a<2
故选C.

练习册系列答案
相关题目
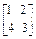 ,求特征值及特征向量.
,求特征值及特征向量.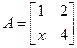 可逆,则
可逆,则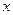 的取值范围为
的取值范围为