题目内容
【题目】某健身馆在2019年7、8两月推出优惠项目吸引了一批客户.为预估2020年7、8两月客户投入的健身消费金额,健身馆随机抽样统计了2019年7、8两月100名客户的消费金额,分组如下:![]() (单位:元),得到如图所示的频率分布直方图:
(单位:元),得到如图所示的频率分布直方图:
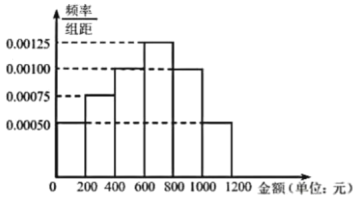
(1)若把2019年7、8两月健身消费金额不低于800元的客户,称为“健身达人”,经数据 处理,现在列联表中得到一定的相关数据,请补全空格处的数据,并根据列联表判断是否有![]() 的把握认为“健身达人”与性别有关?
的把握认为“健身达人”与性别有关?
健身达人 | 非健身达人 | 总计 | |
男 | 10 | ||
女 | 30 | ||
总计 |
(2)为吸引顾客,在健身项目之外,该健身馆特别推出健身配套营养品的销售,现有两种促销方案.
方案一:每满800元可立减100元;
方案二:金额超过800元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
若某人打算购买1000元的营养品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
(3)在(2)中的方案二中,金额超过800元可抽奖三次,假设三次中奖结果互不影响,且三次中奖的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,
的内角,
求证:![]()
附:
|
|
|
|
|
|
|
|
|
|
|
|
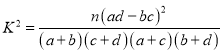
【答案】(1)列联表见解析,有![]() 的把握认为“健身达人”与性别有关系;
的把握认为“健身达人”与性别有关系;
(2)所以选择方案二更划算;
(3)见解析.
【解析】
(1)先根据题目完善表格,再根据公式计算出![]() ,与
,与![]() 比较大小即可得出答案;
比较大小即可得出答案;
(2)若第一个方案,易得付款金额,第二个方案,设付款![]() 元,则
元,则![]() 可能取值为700,800,900,1000,求出分布列,计算出
可能取值为700,800,900,1000,求出分布列,计算出![]() 的期望值,比较大小即可;
的期望值,比较大小即可;
(3)求出至少中一次的概率![]() ,通过
,通过![]() 可得答案.
可得答案.
(1)列联表如下:
健身达人 | 非健身达人 | 总计 | |
男 | 10 | 40 | 50 |
女 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
因为![]() ,
,
因此有![]() 的把握认为“健身达人”与性别有关系;
的把握认为“健身达人”与性别有关系;
(2)若选择方案一:则需付款900元;
若选择方案二:设付款![]() 元,则
元,则![]() 可能取值为700,800,900,1000.
可能取值为700,800,900,1000.
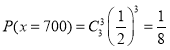 ,
,
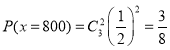 ,
,
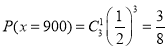 ,
,
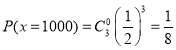 ,
,
所以![]() (元),
(元),
因为![]() ,所以选择方案二更划算;
,所以选择方案二更划算;
(3)∵![]() 是锐角三角形,
是锐角三角形,
∴![]() ,则三次抽奖机会中,该顾客至少中一次的概率为:
,则三次抽奖机会中,该顾客至少中一次的概率为:
![]() 由概率的定义可知:
由概率的定义可知:![]() ,故有:
,故有:
![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案