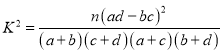题目内容
【题目】已知函数![]() 满足
满足![]() ,若在区间
,若在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,则实数
恰有4个不同的实数解,则实数![]() 的取值范围是___________.
的取值范围是___________.
【答案】![]()
【解析】
由题意,把在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,转化为函数
恰有4个不同的实数解,转化为函数![]() 与
与![]() 的图象在区间
的图象在区间![]() 内有4个不同的交点,作出函数的图象,结合图象,分类讨论,即可求解,得到答案.
内有4个不同的交点,作出函数的图象,结合图象,分类讨论,即可求解,得到答案.
由题意,函数![]() 满足
满足![]() ,即
,即![]() ,即函数
,即函数![]() 是以6为周期的周期函数,
是以6为周期的周期函数,
又由在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,
恰有4个不同的实数解,
即在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,
恰有4个不同的实数解,
即函数![]() 与
与![]() 的图象在区间
的图象在区间![]() 内有4个不同的交点,
内有4个不同的交点,
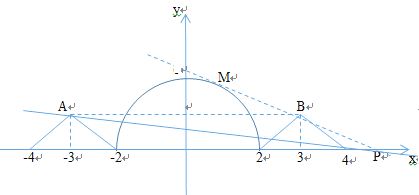
又由函数![]() ,作出函数的图象,如图所示,
,作出函数的图象,如图所示,
由直线![]() ,可知直线恒过点
,可知直线恒过点![]() ,
,
当![]() 时,此时直线
时,此时直线![]() 与函数
与函数![]() 的图象恰有4个交点,
的图象恰有4个交点,
当直线过点![]() 时,此时
时,此时![]() ,即
,即![]() ,此时函数
,此时函数![]() 与直线
与直线![]() 有5个同的交点,
有5个同的交点,
当直线![]() 与半圆
与半圆![]() 相切时,此时圆心到直线
相切时,此时圆心到直线![]() 的距离等于圆的半径,即
的距离等于圆的半径,即![]() ,解得
,解得![]() 或
或![]() (舍去),此时函数
(舍去),此时函数![]() 与直线
与直线![]() 有3个同的交点,
有3个同的交点,
此时函数![]() 与直线
与直线![]() 恰有4个同的交点,则
恰有4个同的交点,则![]()
综上可知,实数![]() 的取值范围是
的取值范围是![]() .
.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案【题目】某健身馆在2019年7、8两月推出优惠项目吸引了一批客户.为预估2020年7、8两月客户投入的健身消费金额,健身馆随机抽样统计了2019年7、8两月100名客户的消费金额,分组如下:![]() (单位:元),得到如图所示的频率分布直方图:
(单位:元),得到如图所示的频率分布直方图:
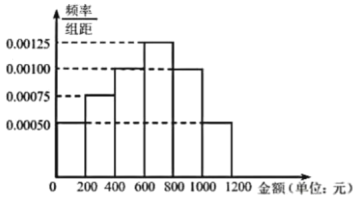
(1)若把2019年7、8两月健身消费金额不低于800元的客户,称为“健身达人”,经数据 处理,现在列联表中得到一定的相关数据,请补全空格处的数据,并根据列联表判断是否有![]() 的把握认为“健身达人”与性别有关?
的把握认为“健身达人”与性别有关?
健身达人 | 非健身达人 | 总计 | |
男 | 10 | ||
女 | 30 | ||
总计 |
(2)为吸引顾客,在健身项目之外,该健身馆特别推出健身配套营养品的销售,现有两种促销方案.
方案一:每满800元可立减100元;
方案二:金额超过800元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
若某人打算购买1000元的营养品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
(3)在(2)中的方案二中,金额超过800元可抽奖三次,假设三次中奖结果互不影响,且三次中奖的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,
的内角,
求证:![]()
附:
|
|
|
|
|
|
|
|
|
|
|
|