题目内容
【题目】已知函数f(x)=alnx-bx2,a,b∈R.若不等式f(x)≥x对所有的b∈(-∞,0],x∈(e,e2]都成立,则实数a的取值范围是( )
A. [e,+∞)B. [![]() ,+∞)
,+∞)
C. [![]() ,e2)D. [e2,+∞)
,e2)D. [e2,+∞)
【答案】B
【解析】
将问题逐步进行转化.由题意得到![]() 对所有的x∈(e,e2]恒成立,由于b≤0,故只需
对所有的x∈(e,e2]恒成立,由于b≤0,故只需![]() 对任意的x∈(e,e2]恒成立,再进一步转化为alnx≥x,即
对任意的x∈(e,e2]恒成立,再进一步转化为alnx≥x,即![]() 对任意的x∈(e,e2]恒成立,只需求出函数
对任意的x∈(e,e2]恒成立,只需求出函数![]() 的最大值即可.
的最大值即可.
由题意可得bx2≤alnx-x对所有的b∈(-∞,0],x∈(e,e2]恒成立,
所以![]() 对所有的x∈(e,e2]恒成立.
对所有的x∈(e,e2]恒成立.
由于b∈(-∞,0],
所以对任意的x∈(e,e2],都有![]() 恒成立,
恒成立,
即alnx≥x对所有的x∈(e,e2]恒成立,
所以![]() 对所有的x∈(e,e2]恒成立.
对所有的x∈(e,e2]恒成立.
令![]() ,则h′(x)=
,则h′(x)=![]() >0,
>0,
所以h(x)在区间(e,e2]上单调递增,
故h(x)max=h(e2)=![]() .
.
所以a≥![]() .
.
所以实数a的取值范围是[![]() ,+∞).
,+∞).
故选B.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】某工厂过去在生产过程中将污水直接排放到河流中对沿河环境造成了一定的污染,根据环保部门对该厂过去10年的监测数据,统计出了其每年污水排放量![]() (单位:吨)的频率分布表:
(单位:吨)的频率分布表:
污水排放量 |
|
|
|
|
频率 | 0.1 | 0.3 | 0.4 | 0.2 |
将污水排放量落入各组的频率作为概率,并假设每年该厂污水排放量相互独立.
(1)若不加以治理,根据上表中的数据,计算未来3年中至少有2年污水排放量不小于200吨的概率;
(2)根据环保部门的评估,该厂当年污水排放量![]() 时,对沿河环境及经济造成的损失为5万元;当年污水排放量
时,对沿河环境及经济造成的损失为5万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为10万元;当年污水排放量
时,对沿河环境及经济造成的损失为10万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为20万元;当年污水排放量
时,对沿河环境及经济造成的损失为20万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
方案1:若该厂不采取治污措施,则需全部赔偿对沿河环境及经济造成的损失;
方案2:若该厂采购治污设备对所有产生的污水净化达标后再排放,则不需赔偿,采购设备的费用为10万元,每年设备维护等费用为15万元,该设备使用10年需重新更换.在接下来的10年里,试比较上述2种方案哪种能为该厂节约资金,并说明理由.
【题目】某健身馆在2019年7、8两月推出优惠项目吸引了一批客户.为预估2020年7、8两月客户投入的健身消费金额,健身馆随机抽样统计了2019年7、8两月100名客户的消费金额,分组如下:![]() (单位:元),得到如图所示的频率分布直方图:
(单位:元),得到如图所示的频率分布直方图:
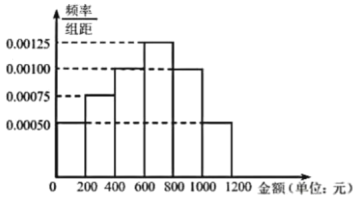
(1)若把2019年7、8两月健身消费金额不低于800元的客户,称为“健身达人”,经数据 处理,现在列联表中得到一定的相关数据,请补全空格处的数据,并根据列联表判断是否有![]() 的把握认为“健身达人”与性别有关?
的把握认为“健身达人”与性别有关?
健身达人 | 非健身达人 | 总计 | |
男 | 10 | ||
女 | 30 | ||
总计 |
(2)为吸引顾客,在健身项目之外,该健身馆特别推出健身配套营养品的销售,现有两种促销方案.
方案一:每满800元可立减100元;
方案二:金额超过800元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
若某人打算购买1000元的营养品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
(3)在(2)中的方案二中,金额超过800元可抽奖三次,假设三次中奖结果互不影响,且三次中奖的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,
的内角,
求证:![]()
附:
|
|
|
|
|
|
|
|
|
|
|
|
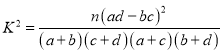
【题目】2018年,南昌市召开了全球VR产业大会,为了增强对青少年VR知识的普及,某中学举行了一次普及VR知识讲座,并从参加讲座的男生中随机抽取了50人,女生中随机抽取了70人参加VR知识测试,成绩分成优秀和非优秀两类,统计两类成绩人数得到如下的列联表:
优秀 | 非优秀 | 总计 | |
男生 | a | 35 | 50 |
女生 | 30 | d | 70 |
总计 | 45 | 75 | 120 |
(1)确定a,d的值;
(2)试判断能否有90%的把握认为VR知识的测试成绩优秀与否与性别有关;
(3)为了宣传普及VR知识,从该校测试成绩获得优秀的同学中按性别采用分层抽样的方法,随机选出6名组成宣传普及小组.现从这6人中随机抽取2名到校外宣传,求“到校外宣传的2名同学中至少有1名是男生”的概率.
附:![]()
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |