题目内容
设正项数列{an}的前n项和为Sn，若{an}和{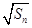
}都是等差数列，且公差相等．
(1)求{an}的通项公式；
(2)若a1，a2，a5恰为等比数列{bn}的前三项，记数列cn＝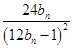
，数列{cn}的前n项和为Tn.求证：对任意n∈N*，都有Tn<2.
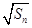}都是等差数列，且公差相等．(1)求{an}的通项公式；
(2)若a1，a2，a5恰为等比数列{bn}的前三项，记数列cn＝
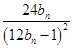，数列{cn}的前n项和为Tn.求证：对任意n∈N*，都有Tn<2.(1) an＝
(2)见解析
(2)见解析解：(1)设{an}的公差为d，
则＝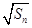
＝
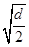·n，且a1－
＝0.
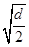又d＝，所以d＝
，
a1＝＝
，an＝.
(2)证明：易知bn＝×3n－1，
∴cn＝
.
当n≥2时， <
＝
＝
－
，
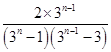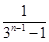∴当n≥2时，Tn＝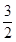
＋
＋…＋<＋
＋
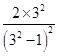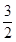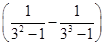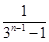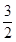＋…＋－＝2－<2，且T1＝<2，
故对任意n∈N*，都有Tn<2.
则
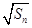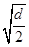＝＝·n，且a1－＝0.又d＝
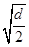，所以d＝，a1＝
＝，an＝.(2)证明：易知bn＝
×3n－1，∴cn＝
.当n≥2时，
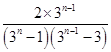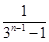<＝＝－，∴当n≥2时，Tn＝
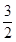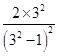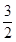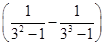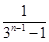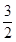＋＋…＋<＋＋＋…＋－＝2－<2，且T1＝<2，故对任意n∈N*，都有Tn<2.
练习册系列答案
阅读快车系列答案
相关题目
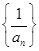是等差数列并求数列{an}的通项公式；
.
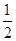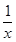(x>0)及两点A1(x1,0)和A2(x2,0)，其中x2>x1>0.过A1，A2分别作x轴的垂线，交曲线C于B1，B2两点，直线B1B2与x轴交于点A3(x3,0)，那么( )
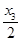，x2成等差数列
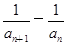＝d(n∈N*，d为常数)，则称数列{an}为“调和数列”．已知正项数列
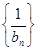为“调和数列”，且b1＋b2＋…＋b9＝90，则b4·b6的最大值是( )．
中，
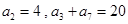，则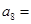
( )