题目内容
若数列{an}满足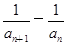
＝d(n∈N*，d为常数)，则称数列{an}为“调和数列”．已知正项数列
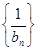为“调和数列”，且b1＋b2＋…＋b9＝90，则b4·b6的最大值是( )．
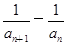＝d(n∈N*，d为常数)，则称数列{an}为“调和数列”．已知正项数列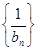为“调和数列”，且b1＋b2＋…＋b9＝90，则b4·b6的最大值是( )．| A．10 | B．100 | C．200 | D．400 |
B
由已知得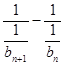
＝d，即bn＋1－bn＝d，
∴{bn}为等差数列，由b1＋b2＋…＋b9＝90，得9b5＝90，b5＝10，b4＋b6＝20，又bn>0，所以b4·b6≤
2＝100，当且仅当b4＝b6＝10时，等号成立．
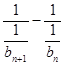＝d，即bn＋1－bn＝d，∴{bn}为等差数列，由b1＋b2＋…＋b9＝90，得9b5＝90，b5＝10，b4＋b6＝20，又bn>0，所以b4·b6≤
2＝100，当且仅当b4＝b6＝10时，等号成立．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
}都是等差数列，且公差相等．
，数列{cn}的前n项和为Tn.求证：对任意n∈N*，都有Tn<2.
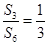，则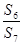
＝________.
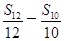＝2，则S2 014的值等于( )．
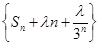为等差数列？若存在，求出λ的值；若不存在，则说明理由．