题目内容
18．已知正方体ABCD-A1B1C1D1的棱长为3，点O在棱AA1上，且OA1=2OA，平面α过点O且垂直于AA1，点P在平面α内，PQ⊥A1C1于点Q．若PA=PQ，则P点的轨迹是（ ）| A． | 圆 | B． | 椭圆 | C． | 抛物线 | D． | 两条直线 |
分析 在对角面A1C1中，利用PQ⊥A1C1于点Q，PA=PQ，可得P到定点A的距离等于P到定直线A1C1的距离，利用抛物线的定义，即可得出P点的轨迹．
解答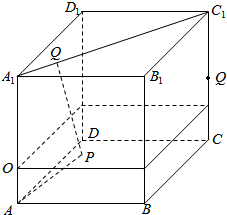 
解：由题意，在对角面A1C1中，∵PQ⊥A1C1于点Q，PA=PQ，
∴P到定点A的距离等于P到定直线A1C1的距离，
∴P点的轨迹是抛物线．
故选：C．
点评 本题考查轨迹方程，考查抛物线的定义，正确运用抛物线的定义是关键．
练习册系列答案
相关题目
13．在三棱锥P-ABC中，平面PAB⊥平面ABC，PA=PB，AC⊥BC，AB=4，PC=6，则三棱锥P-ABC的外接球O的表面积为（ ）
| A． | $\frac{81π}{2}$ | B． | 41π | C． | 32$\sqrt{2}$π | D． | 32π |
7．设ω＞0，m＞0，若函数f（x）=msin$\frac{ωx}{2}$cos$\frac{ωx}{2}$在区间[-$\frac{π}{3}$，$\frac{π}{3}$]上单调递增，则ω的取值范围是（ ）
| A． | （0，$\frac{2}{3}$） | B． | （0，$\frac{3}{2}$] | C． | [$\frac{3}{2}$，+∞） | D． | [1，+∞） |