题目内容
10.已知tanα=-$\frac{3}{4}$,计算:(1)$\frac{3sinα+2cosα}{sinα-4cosα}$;
(2)2sin2α+3sinαcosα
分析 利用三角函数的基本关系式--商数关系、平方关系将式子变形为关于正切的式子求值.
解答 解:(1)$\frac{3sinα+2cosα}{sinα-4cosα}$=$\frac{3tanα+2}{tanα-4}=\frac{3×(-\frac{3}{4})+2}{-\frac{3}{4}-4}$=$\frac{1}{19}$;
(2)2sin2α+3sinαcosα=$\frac{2si{n}^{2}α+3sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{2ta{n}^{2}α+3tanα}{ta{n}^{2}α+1}$=$\frac{2×\frac{9}{16}-3×\frac{3}{4}}{\frac{9}{16}+1}$=$-\frac{18}{25}$.
点评 本题考查了三角函数齐次式的化简求值,利用了三角函数的商数关系.

练习册系列答案
相关题目
1.在Rt△ABC中,已知D是斜边AB上任意一点(如图①),沿直线CD将△ABC折成直二面角B-CD-A(如图②).若折叠后A,B两点间的距离为d,则下列说法正确的是 ( )
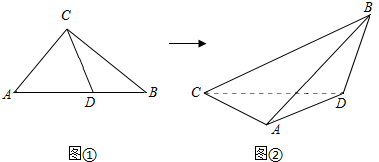

| A. | 当CD为Rt△ABC的中线时,d取得最小值 | |
| B. | 当CD为Rt△ABC的角平分线时,d取得最小值 | |
| C. | 当CD为Rt△ABC的高线时,d取得最小值 | |
| D. | 当D在Rt△ABC的AB边上移动时,d为定值 |
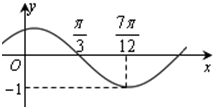 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.