题目内容
3．已知集合A={2，3}，B={x|x2+ax+4=0}，且A∩B=B，求a的取值范围．分析 求解一元二次方程化简集合A，由A∩B=B得B⊆A，然后分B为空集、单元素集合、双元素集合分类求解满足条件的a的范围，最后取并集得答案．
解答 解：由A∩B=B，得B⊆A．
若a2-16＜0，即-4＜a＜4，B=∅，满足B⊆A；
若a2-16=0，即a=±4，a=-4，B={2}，满足B⊆A；a=4，B={-2}，不满足B⊆A；
若a2-16＞0，即a＜-4或a＞4，要使B⊆A，则2，3为方程x2+ax+4=0的两根，此时不成立．
∴满足B∩A=B的a的取值范围是-4≤a＜4．
点评 本题考查了集合间的关系，考查了交集及其运算，考查了分类讨论的数学思想方法，是基础题．
练习册系列答案
相关题目
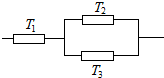三个元件T1，T2，T3正常工作的概率分别为$\frac{1}{2}$，$\frac{3}{4}$，$\frac{3}{4}$，且是互相独立的．将它们中某两个元件并联后再和第三元件串联接入电路，在如图的电路中，电路不发生故障的概率是$\frac{15}{32}$．
15．若0＜α＜$\frac{π}{2}$，0＜β$＜\frac{π}{2}$，且tanα=$\frac{1}{7}$，tanβ=$\frac{3}{4}$，求证：α+β=$\frac{π}{4}$．