题目内容
1.在Rt△ABC中,已知D是斜边AB上任意一点(如图①),沿直线CD将△ABC折成直二面角B-CD-A(如图②).若折叠后A,B两点间的距离为d,则下列说法正确的是 ( )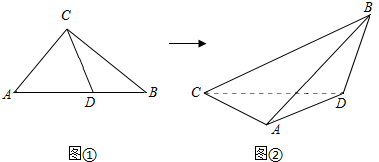
| A. | 当CD为Rt△ABC的中线时,d取得最小值 | |
| B. | 当CD为Rt△ABC的角平分线时,d取得最小值 | |
| C. | 当CD为Rt△ABC的高线时,d取得最小值 | |
| D. | 当D在Rt△ABC的AB边上移动时,d为定值 |
分析 过A作CD的垂线AG,过B作CD的延长线的垂线BH,设BC=a,AC=b,∠ACD=θ,利用两条异面直线上两点间的距离转化为含有θ的三角函数求得最值.
解答 解:如图,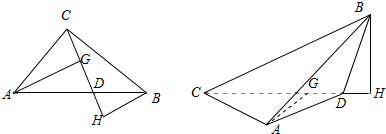
设BC=a,AC=b,∠ACD=θ,则$∠BCD=\frac{π}{2}-θ$(0$<θ<\frac{π}{2}$),
过A作CD的垂线AG,过B作CD的延长线的垂线BH,
∴AG=bsinθ,BH=acosθ,CG=bcosθ,CH=asinθ,则HG=CH-CG=asinθ-bcosθ,
∴d=|AB|=$\sqrt{A{G}^{2}+B{H}^{2}+H{G}^{2}}$=$\sqrt{{b}^{2}si{n}^{2}θ+{a}^{2}co{s}^{2}θ+(asinθ-bcosθ)^{2}}$
=$\sqrt{{b}^{2}si{n}^{2}θ+{a}^{2}co{s}^{2}θ+{a}^{2}si{n}^{2}θ+{b}^{2}co{s}^{2}θ-absin2θ}$=$\sqrt{{a}^{2}+{b}^{2}-absin2θ}$.
∴当$θ=\frac{π}{4}$,即当CD为Rt△ABC的角平分线时,d取得最小值.
故选:B.
点评 本题考查平面与平面之间的位置关系,考查了两条异面直线上两点间的距离,运用数学转化思想方法是解答该题的关键,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.若0<α<$\frac{π}{2}$,0<β$<\frac{π}{2}$,且tanα=$\frac{1}{7}$,tanβ=$\frac{3}{4}$,求证:α+β=$\frac{π}{4}$.
12.下列命题:
①有一个角等于30°的两个等腰三角形相似;
②有一个角等于120°的两个等腰三角形相似;
③相似三角形一定是全等三角形;
④相似三角形对应角的平分线的比等于周长比.
其中正确命题的个数是( )
①有一个角等于30°的两个等腰三角形相似;
②有一个角等于120°的两个等腰三角形相似;
③相似三角形一定是全等三角形;
④相似三角形对应角的平分线的比等于周长比.
其中正确命题的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
6.已知实数x,y满足$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{0≤y≤6}\end{array}\right.$,若z=x+y,则z的取值范围是( )
| A. | [-12,6] | B. | [-6,12] | C. | [-3,12] | D. | [6,12] |
13.一对父子参加一个亲子摸奖游戏,其规则如下:父亲在装有红色、白色球各两个的甲袋子里随机取两个球,儿子在装有红色、白色、黑色球各一个的乙袋子里随机取一个球,父子俩取球相互独立,两人各摸球一次合在一起称为一次摸奖,他们取出的三个球的颜色情况与他们获得的积分对应如下表:
(Ⅰ)求一次摸奖中,所取的三个球中恰有两个是红球的概率;
(Ⅱ)设一次摸奖中,他们所获得的积分为X,求X的分布列及均值(数学期望)E(X).
| 所取球的情况 | 三个球均为红色 | 三个球均不同色 | 恰有两球为红色 | 其他情况 |
| 所获得的积分 | 180 | 90 | 60 | 0 |
(Ⅱ)设一次摸奖中,他们所获得的积分为X,求X的分布列及均值(数学期望)E(X).
11.下列各组对象中可以组成集合的是( )
| A. | 所有著名的歌手 | B. | 小于3的自然数 | ||
| C. | 高二•(1)班中所有高个子的男生 | D. | 花园中很漂亮的花 |