题目内容
【题目】已知函数![]() 在
在![]() 处取得极值,且在
处取得极值,且在![]() 处的切线的斜率为
处的切线的斜率为![]() .
.
(1) 求![]() 的解析式;
的解析式;
(2) 求过点![]() 的切线方程.
的切线方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)由函数![]() 在
在![]() 处取得极值,且在
处取得极值,且在![]() 处的切线的斜率为
处的切线的斜率为![]() ,求出导函数,可得
,求出导函数,可得![]() 是
是![]() 的两根,且
的两根,且![]() ,解方程组即可求得
,解方程组即可求得![]() 的值,从而求得
的值,从而求得![]() 的解析式;(2)设切点,求切线方程,将点
的解析式;(2)设切点,求切线方程,将点![]() 切线方程得到
切线方程得到![]() ,解方程可得
,解方程可得![]() ,从可得切线斜率,运用点斜式方程,进而得到所求切线的方程.
,从可得切线斜率,运用点斜式方程,进而得到所求切线的方程.
试题解析:(1)函数f(x)=ax3+bx2+cx的导数为f'(x)=3ax2+2bx+c, 依题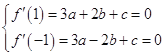 ,
,
又f'(0)=﹣3即c=﹣3 ∴a=1,b=0, ∴f(x)=x3﹣3x
(2)解:设切点为(x0 , x03﹣3x0), ∵f'(x)=3x2﹣3∴切线的斜率为f'(x0)=3x02﹣3,∴切线方程为y﹣(x03﹣3x0)=(3x02﹣3)(x﹣x0),
又切线过点A(2,2),
∴2﹣(x03﹣3x0)=(3x02﹣3)(2﹣x0),
∴2x03﹣6x02+8=0,即为2(x0+1)(x0﹣2)2=0, 解得x0=﹣1或2,
可得过点A(2,2)的切线斜率为0或9,
即有过点A(2,2)的切线方程为y﹣2=0或y﹣2=9(x﹣2),
即为y﹣2=0或9x﹣y﹣16=0 .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目