题目内容
【题目】在直角坐标系xOy中，圆C的参数方程为
（α为参数），以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系．
（1）写出圆C的极坐标方程及圆心C的极坐标；
（2）直线l的极坐标方程为
与圆C交于M，N两点，求△CMN的面积．
【答案】（1）
，圆心C（2，
）（2）
【解析】分析：（1）先根据三角形同角关系消参数得圆C圆心直角坐标以及圆方程的直角坐标方程，再根据
将直角坐标化为极坐标，（2）将直线极坐标方程代入圆极坐标方程得交点极坐标，再根据三点极坐标关系求三角形面积.
详解：（1）极坐标（ρ，θ）与直角坐标（x，y）的对应关系为：
，
所以
，
根据sin2α+cos2α=1，消元得（
）2﹣（ρsinθ﹣1）2=4，
化简得：．
因为圆心C直角坐标为（，1），∴极坐标为（2，）．
（2）联立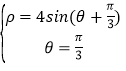
，得交点极坐标M（0，0），N（2，
），
所以|MN|=2，|MC|=2，
所以△CMN的面积．
练习册系列答案
相关题目
