题目内容
【题目】在△ABC中，角A，B，C的对边分别为 
． （Ⅰ）求cosB的值；
（Ⅱ）若 
，求a和c的值．
【答案】解：（Ⅰ）∵cos 
= 
， ∴sin 
=sin（ 
﹣ ）= ，
∴cosB=1﹣2sin2 = 
．
（Ⅱ）由 
=2可得 accosB=2，又cosB= ，
故ac=6，
由 b2=a2+c2﹣2accosB 可得a2+c2=12，
∴（a﹣c）2=0，
故 a=c，
∴a=c= 
【解析】（1）利用诱导公式求出sin 
的值，从而利用二倍角的余弦公式求得cosB．（2）由两个向量的数量积的定义求出ac的值，再利用余弦定理求出a和c的值．
【考点精析】认真审题，首先需要了解同角三角函数基本关系的运用(同角三角函数的基本关系：
；
;（3） 倒数关系：
)，还要掌握余弦定理的定义(余弦定理:
;
;
)的相关知识才是答题的关键．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】某工厂生产不同规格的一种产品，根据检测标准，其合格产品的质量
与尺寸
之间满足关系式
（
为大于0的常数），现随机抽取6件合格产品，测得数据如下：
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
（1）求
关于
的回归方程；（提示：
与
有线性相关关系）
（2）按照某项指标测定，当产品质量与尺寸的比在区间
内时为优等品，现从抽取的6件合格产品再任选3件，求恰好取得两件优等品的概率.
参考数据及公式：
，
，
，
对于样本
（
），其回归直线
的斜率和截距的最小二乘估计公式分别为：
，
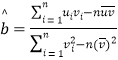