题目内容
【题目】如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB. 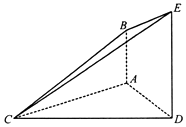
(I)求证:平面BCE⊥平面CDE;
(II)求平面BCE与平面ADEB所成锐二面角的余弦值.
【答案】(Ⅰ)证明:取CD的中点F,EC的中点P,连接BP,PF, 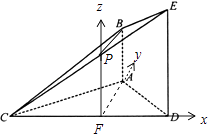
∴PF∥ED,PF= ![]() ,
,
由已知得,AB∥DE,AB= ![]() DE,
DE,
∴AB∥PF,AB=PF,则四边形ABPF为平行四边形,得BP∥AF,
∵AB∥DE,AB⊥平面ACD,∴DE⊥平面ACD,
又AF平面ACD,∴AF⊥ED.
又△ACD是等腰三角形,F是CD的中点,∴AF⊥CD.
∴BP⊥DE,BP⊥CD,又DE∩CD=D,∴BP⊥平面CDE.
又BP平面BCE,∴平面BCE⊥平面CDE;
(Ⅱ)解:以F为坐标原点,分别以FD、FA、FP所在直线为x、y、z轴建立空间直角坐标系,
设AD=2,∵∠CAD=120°,∴CD= ![]() ,
,
则C( ![]() ,0,0),D(
,0,0),D( ![]() ,0,0),A(0,1,0),B(0,1,1),E(
,0,0),A(0,1,0),B(0,1,1),E( ![]() ,0,2).
,0,2).
∴ ![]() ,
,
设平面BCE的一个法向量为 ![]() ,
,
则  ,取x=1,得
,取x=1,得 ![]() .
.
又 ![]() ,
, ![]() .
.
设平面ADEB的一个法向量 ![]() ,
,
则 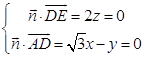 ,令x=1,得
,令x=1,得 ![]() .
.
设平面BCE与平面ADEB所成的锐角为θ,
则cosθ=|cos< ![]() >|=
>|= ![]() .
.
【解析】(Ⅰ)取CD的中点F,EC的中点P,连接BP,PF,由已知结合三角形中位线定理可得四边形ABPF为平行四边形,得BP∥AF,进一步求得DE⊥平面ACD,得到AF⊥ED.再由△ACD是等腰三角形,F是CD的中点,得到AF⊥CD.由线面垂直的判定可得BP⊥平面CDE.则平面BCE⊥平面CDE;(Ⅱ)以F为坐标原点,分别以FD、FA、FP所在直线为x、y、z轴建立空间直角坐标系,由已知求出所用点的坐标,得到平面BCE与平面ADEB的一个法向量,由两法向量所成角的余弦值可得平面BCE与平面ADEB所成锐二面角的余弦值.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.


