题目内容
【题目】若非零向量 ![]() 与向量
与向量 ![]() 的夹角为钝角,
的夹角为钝角, ![]() ,且当
,且当 ![]() 时,
时, ![]() (t∈R)取最小值
(t∈R)取最小值 ![]() .向量
.向量 ![]() 满足
满足 ![]() ,则当
,则当 ![]() 取最大值时,
取最大值时, ![]() 等于( )
等于( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,如图: ∵向量
,如图: ∵向量 ![]() ,
, ![]() 的夹角为钝角,
的夹角为钝角,
∴当 ![]() 与
与 ![]() 垂直时,
垂直时, ![]() 取最小值
取最小值 ![]() ,即
,即 ![]() .
.
过点B作BD⊥AM交AM延长线于D,则BD= ![]() ,
,
∵| ![]() |=MB=2,∴MD=1,∠AMB=120°,即
|=MB=2,∴MD=1,∠AMB=120°,即 ![]() 与
与 ![]() 夹角为120°.
夹角为120°.
∵ ![]() ,∴
,∴ ![]() (
( ![]() )=0,
)=0,
∴| ![]() ||
|| ![]() |cos120°+
|cos120°+ ![]() |
| ![]() |2=0,
|2=0,
∴| ![]() |=2,即MA=2,
|=2,即MA=2,
∵ ![]() ,∴
,∴ ![]() 的终点C在以AB为直径的圆O上,
的终点C在以AB为直径的圆O上,
∵O是AB中点,∴ ![]() =2
=2 ![]() ,
,
∴当M,O,C三点共线时, ![]() 取最大值,
取最大值,
∵AB= ![]() =2
=2 ![]() ,∴OB=0C=
,∴OB=0C= ![]() =
= ![]() ,
,
∵MA=MB=2,O是AB中点,∴MO⊥AB,
∴∠BOC=∠MOA=90°,
∴| ![]() |=BC=
|=BC= ![]() OB=
OB= ![]() .
.
故选:A.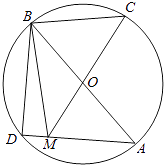

练习册系列答案
相关题目
【题目】某工厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间满足关系式
之间满足关系式![]() (
(![]() 为大于0的常数),现随机抽取6件合格产品,测得数据如下:
为大于0的常数),现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
(1)求![]() 关于
关于![]() 的回归方程;(提示:
的回归方程;(提示:![]() 与
与![]() 有线性相关关系)
有线性相关关系)
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率.
内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率.
参考数据及公式:
![]() ,
,![]() ,
,![]() ,
,![]()
对于样本![]() (
(![]() ),其回归直线
),其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
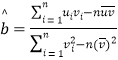 ,
,![]()

