题目内容
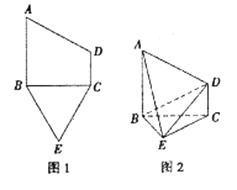
【题目】如图，在正方体ABCD－ABCD中,平面
垂直于对角线AC,且平面截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则（ ）
A. S为定值,l不为定值 B. S不为定值,l为定值
C. S与l均为定值 D. S与l均不为定值
【答案】B
【解析】
将正方体切去两个正三棱锥
和
，得到一个几何体
，是以平行平面
和
为上下底，每个侧面都是直角等腰三角形，截面多边形的每一条边分别与的底面上的一条边平行，设正方体棱长为
，
，可求得六边形的周长为
与
无关，即周长为定值；当
都在对应棱的中点时，
是正六边形，计算可得面积
，当无限趋近于时，的面积无限趋近于
，从而可知的面积一定会发生变化。
设平面
截得正方体的六个表面得到截面六边形为，与正方体的棱的交点分别为（如下图），
将正方体切去两个正三棱锥和，得到一个几何体，是以平行平面和为上下底，每个侧面都是直角等腰三角形，截面多边形的每一条边分别与的底面上的一条边平行，设正方体棱长为，，则
，
，故
，同理可证明
，故六边形的周长为，即周长为定值；
当都在对应棱的中点时，是正六边形，计算可得面积
，三角形的面积为
，当无限趋近于时，的面积无限趋近于，故的面积一定会发生变化，不为定值。
故答案为B.
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
